Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » výpočet pol.kruhu,když znám délku tětivy a vzdal.tětivy od kraje kruhu
#1 09. 05. 2011 15:57
výpočet pol.kruhu,když znám délku tětivy a vzdal.tětivy od kraje kruhu
Zdravím....už jsem nějaké desítky let ze školy a potřebuji vypočítat něco ve stavebnictví,co souvisí z geometrií..na stavbě potřebuji udělat otvory pro okno,kde nad různě širokými okny bude oblouk vždy vysoký 15 cm...to znamená,že ve středu okna bude oblouk vysoký 15 cm,na okraji 0 cm....To znamená,že potřebuji vědět délku poloměru kruhu...např pro šířku okna 1metr bude menší poloměr,než pro šířku okna třeba 150 cm...Výška oblouku vždy musí být 15 cm...potřebuji nějaký vzorec a vysvětlení,jak to udělat...moc děkuji za pomoc
Offline
#2 09. 05. 2011 16:38 — Editoval Hanis (09. 05. 2011 16:44)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: výpočet pol.kruhu,když znám délku tětivy a vzdal.tětivy od kraje kruhu
Tak z Pythagorovy věty: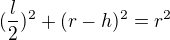
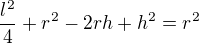
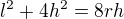
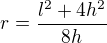
Kde r je hledaný poloměr, h je "výška" oblouku (15cm) a l délka tětivy. Bacha na jednotky.
Offline
#3 09. 05. 2011 16:39 — Editoval Rumburak (09. 05. 2011 16:42)
Re: výpočet pol.kruhu,když znám délku tětivy a vzdal.tětivy od kraje kruhu
↑ hup:
Je tedy dána úsečka  délky
délky  (šířka okna) a tato úsečka má být tětivou jakési kružnice
(šířka okna) a tato úsečka má být tětivou jakési kružnice  o neznámém poloměru
o neznámém poloměru  .
.
Nechť  je střed kružnice
je střed kružnice  a
a  střed ús.
střed ús.  . Potom trojúhelník
. Potom trojúhelník 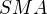 je pravoúhlý (pravý úhel při vrcholu
je pravoúhlý (pravý úhel při vrcholu  ).
).
Jeho přepona  má délku
má délku  rovnou poloměru kružnice
rovnou poloměru kružnice  . Pythagorova věta dává
. Pythagorova věta dává
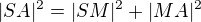 ,
,
neboli
(1) 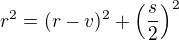 .
.
kde 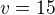 je požadovaná výška kruhové úseče tvořící "lunetu" nad oknem. Rovnice (1) má řešení
je požadovaná výška kruhové úseče tvořící "lunetu" nad oknem. Rovnice (1) má řešení
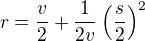 .
.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » výpočet pol.kruhu,když znám délku tětivy a vzdal.tětivy od kraje kruhu