Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 05. 2011 10:04 Příspěvek uživatele M0M0 byl skryt uživatelem M0M0.
#3 12. 05. 2011 10:16
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Dôkaz sporom
↑ M0M0:
ten druhý příklad smaž a založ na něj nové téma...
Víš, jak se řeší důkazy sporem?
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#4 12. 05. 2011 10:19 — Editoval musixx (12. 05. 2011 10:21)
Re: Dôkaz sporom
Asi vhodnější je mít na každou úlohu separátní téma...
1. Sporem předpokládejme, že existují taková kladná reálná a a b, že  . Pak... zvládneš pokračovat tak, abys došel k nějakému zjevně nepravdivému tvrzení?
. Pak... zvládneš pokračovat tak, abys došel k nějakému zjevně nepravdivému tvrzení?
2. Vem levou stranu, vytkni, co jde, upravuj a čekej, až z toho vznikne strana pravá... A nejde moc o kombinatoriku.
Offline
#5 12. 05. 2011 10:36 — Editoval M0M0 (12. 05. 2011 10:39)
Re: Dôkaz sporom
1. Jasné, že viem ako sa to robí, len to momentálne nestíham :/ sporom spravíš negáciu a dokazuješ priamo-logická postupnosť, čiže T1,T2,T3....Tn - kde posledné je dokazovaný výrok..lenže momentálne je to nestíhačka...
2. s tým ani nepohnem
tie prvé kroky som zvládol aj sám, len sa s tým nestíham hrať... :/ bohužial
proste potrebujem to čím skôr, ja si v tom už logiku nájdem...
Offline
#7 12. 05. 2011 11:07 — Editoval M0M0 (12. 05. 2011 11:08)
Re: Dôkaz sporom
Výborne - prvý som pochopil...čiže si len vynasobil a.b prvého jednočlena...a ekvivalentne aj pravu stranu - vznikol vzorec...po uprave další, ktorý má v exponente 2 čiže bude vždy kladný a to je v rozpozpore s podmienkou..správne? :)
a ten druhý zatial analyzujem...
Offline



 ,
,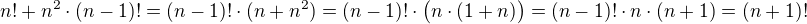 .
.