Matematické Fórum

lenovotna · 15. 05. 2011 16:22

Ahoj prosím o radu, mám příklad: náhodná veličina X má distribuční funkci
F(x) = k + (l / 1+x^2) pro 0<x<nekonečno; a 0 pro x menší nebo rovno 0
mám spočítat konstanty k a l, hustotu a pravděpodobnost,
bohužel nevím jak na ty konstanty, děkuji za radu!!!

halogan · 15. 05. 2011 16:39

Jaka je limita F pro x jdouci k nekonecnu?

lenovotna · 15. 05. 2011 16:46

↑ halogan:

limita F pro x jdouci k nekonecnu je 0 ???

halogan · 15. 05. 2011 17:35

↑ lenovotna:

To by trochu odporovalo definici. Zkuste to ještě jednou.

$F_X(x) = P (X < x)$

lenovotna · 15. 05. 2011 17:36

↑ halogan:

já si s tím opravdu nevím rady a potřebuji nějaký postup prosím

halogan · 15. 05. 2011 18:22

Pokud budeme z našeho samplu brát stále víc a víc hodnot (x jde do nekonečna), tak se bude pravděpodobnost jevu zvyšovat, ne?

lenovotna · 15. 05. 2011 18:25

↑ halogan:

ano

halogan · 15. 05. 2011 18:34

↑ lenovotna:

A pokud budeme stále dál do nekonečna, tak už ten jev bude skoro jistý, že?

Chápete, kam mířím?

lenovotna · 15. 05. 2011 18:44

↑ halogan:

že se to rovná 1 ??

halogan · 15. 05. 2011 19:23

Přesně tak. Ono se to nemusí vyloženě rovnat, ale jde to limitně k jedničce určitě.

Tak teď spočtěte tu zadanou limitu i s těma konstantama. Kolik vyjde?

lenovotna · 15. 05. 2011 19:25

↑ halogan:

a to je to co nevím, kdybych věděla jak to spočíst i s konstantama tak se neptám...bohužel ty limity jak se počítají abych dostala k a l nevím?

halogan · 15. 05. 2011 19:31

↑ lenovotna:

Tak kolik je tohle: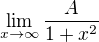

$\lim_{x \to \infty} \frac{A}{1 + x^2}$ , kde K je nějaké reálné číslo.

lenovotna · 15. 05. 2011 19:44

↑ halogan:

netuším proto se ptám na postup

halogan · 15. 05. 2011 21:26

↑ lenovotna:

Tohle je limita z posledního ročníků SŠ.

V čitateli máme nějakou stálou hodnotu, jmenovatel roste nad všechny meze... kam taková hodnota směruje?

Co když nějaký objekt (A) dělíte na stále více a více kousků? Jak velké ty kousky budou?

Matematické Fórum

#1 15. 05. 2011 16:22

distribuční funkce

#2 15. 05. 2011 16:39

Re: distribuční funkce

#3 15. 05. 2011 16:46

Re: distribuční funkce

#4 15. 05. 2011 17:35

Re: distribuční funkce

#5 15. 05. 2011 17:36

Re: distribuční funkce

#6 15. 05. 2011 18:22

Re: distribuční funkce

#7 15. 05. 2011 18:25

Re: distribuční funkce

#8 15. 05. 2011 18:34

Re: distribuční funkce

#9 15. 05. 2011 18:44

Re: distribuční funkce

#10 15. 05. 2011 19:23

Re: distribuční funkce

#11 15. 05. 2011 19:25

Re: distribuční funkce

#12 15. 05. 2011 19:31

Re: distribuční funkce

#13 15. 05. 2011 19:44

Re: distribuční funkce

#14 15. 05. 2011 21:26

Re: distribuční funkce

Zápatí