Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 21. 05. 2011 16:11 — Editoval BakyX (21. 05. 2011 16:12)
Re: Zápis pomocou sigma
↑ Phate:
Myslím, že áno.
↑ OiBobik:
Dvojitá suma mi príde elegantnejšie. To tvoje jednoduchšie nemôžem použiť, lebo to je predsa návod na riešenie :)
Vybral som si: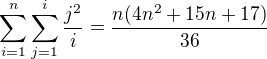
Trocha divné, že je to úloha s *
Ďakujem obom :)
EIDT: Chcem sa ešte spýtať, či niekto nepozná nejaký zdroj príkladov na takéto (prípadne kombinatorické) sumy, ktoré sa dajú riešiť metódami bez matematckej analýzy. Ďakujem
1^6 - 2^6 + 3^6 = 666
Offline

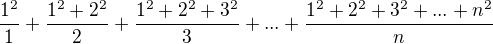
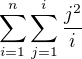 Mohlo by to byt takhle?
Mohlo by to byt takhle?
