Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 05. 2011 17:00
priklady k maturite
1) Určete nejmenší hodnotu proměnné x+1 = (sqrt(x+5)-2) (sqrt(x+5)+2) .
u tohoto si nejsem jist protoze pokud bych resil rovnici tak v ty odmocnine musi platit podminka ze x+5 > 0 x muuze byt nejmensi hodnota -5? ale zase pokud bych to algebraicky upravil tak mi vyslo reseni cela mnozina cisel ale zase vidim ze je to blbost. protoze minus v odmocnine nejde. vyslesky prave k tomu nemam takze si nejsem jist u reseni.
2)Úloha 20 max. 3b.
Hází se dvěma hracími kostkami s 1, 2 až 6 oky na stěnách. Označme následující jevy:
J: Počty ok, které padnou na obou kostkách, se liší o jednotku.
D: Počty ok, které padnou na obou kostkách, se liší o dvě.
T: Počty ok, které padnou na obou kostkách, se liší o tři.
S: Na obou kostkách padne stejný počet ok.
Pravděpodobnosti jednotlivých jevů označme po řadě PJ, PD, PT, PS.
Rozhodněte, jsou-li následující tvrzení pravdivá (ANO), nebo nepravdivá (NE).
20.1 P(S) = 1/6 (ANO–NE)
20.2 P(J) > P(D) (ANO–NE)
20.3 P(S) =! P(T) (ANO–NE)
20.4 P(D)= P(T) (ANO–NE)
zde bych poprosil i reseni cele. My jeste nebrali kombinace,pravdepodobnost a nic takoveho (mame to az ve 4 roc.).
Offline
- (téma jako vyřešené označil(a) Dana1)
#2 27. 05. 2011 17:11
Re: priklady k maturite
↑ Annnnnd:
ad 1)
o to právě jde, dát dohromady algebraické řešení (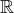 ) a podmínky.
) a podmínky.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 27. 05. 2011 23:33
Re: priklady k maturite
↑ Annnnnd:
A co je konkrétně problém? Spočítat ty pravděpodobnosti?
Na ukázku J: příznivé možnosti 1-2, 2-3, 3-4, 4-5, 5-6 a obráceně, tj. celkem 10 příznivých možností. Všech možností je 36.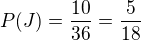
Zbylé jevy naprosto stejně.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
