Matematické Fórum

studen1 · 28. 05. 2008 15:49

Zdravim všechny matematické zoufalce a klaním se přede všemi, kteří tu matematicky radí (nejednou mi vaše rady pomohli pochopit látku, by? jsem žádný dotaz ještě neměl), prosil bych o pomoc s následujícím příkladem:

Součtem řady 1 + 2x + 3x2 + ... + nxn–1 + ... je pro x  (–1; 1) a) ln(1+x) b) 1/(1–x) c) 1/(1–x)2 d) cotgx

mě pořád vychází 1/(1–x) po dosazení do vzorce s=a1/(1–q) , problem je, že má asi vyjít 1/(1–x)2 .

Napadlo mě, žemožná blbě určuji a1 jako 1 a mělo by to být x,ale pak by mi to nevycházelo...
Předem děkuji za lehké matematické na?uknutí

roman0159 · 28. 05. 2008 16:33

Ale to nie je geometrický rad, čiže ten vzorec Ti nepomôže. Asi to treba urobi? cez Taylorov polynóm...

plisna · 28. 05. 2008 17:00 — Editoval plisna (28. 05. 2008 17:02)

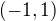uvazujme mocninnou radu $1 + 2x + 3x^2 + 4x^3 + \dots$ , ktera je na intervalu $(-1, 1)$ stejnomerne konvergentni. pak ji lze integrovat clen po clenu a dostavame radu $x + x^2 + x^3 + \dots$ , coz je pro $x \in (-1, 1)$ geometricka rada s $a_0 = x, \quad q = x$ . jeji soucet je tedy $s = \frac{x}{1-x}$ . zajima-li nas soucet rady puvodni, musime tento vztah zderivovat a dostavame reseni $s = \frac{1}{(1-x)^2}$ . polomer konvergence se nezmeni, je nutne vsak overit konvergenci v krajnich bodech. pokud si toto vlakno precte Marian, urcite sem doplni dalsi poznamky o konvergenci ci postupu.

studen1 · 28. 05. 2008 17:12

Moc děkuji za radu, už do skript koukám moc dlouho v kuse :-) Tak jsem to bral automaticky jako geom. posloupnost.

studen1 · 07. 06. 2008 13:32

Považuji za slušnost poděkovat, takž děkuji všem za rady v tomto foru, vyústilo to v úspěšnou zkoušku. Zejmena pak panu Maříkovi, jehož slidy mi hodně pomohli. Jen tak dál ;)

Marian · 07. 06. 2008 22:24 — Editoval Marian (07. 06. 2008 22:24)

↑ plisna:

Dekuju za tu duveru, ze ja jsem ten, ktery by snad mohl neco doplnit.

Snad jen podotknu, ze pokud vyse uvedene nebylo brano, je mozne aplikovat postup jednodussi (ale zase jine kroky budou mene snadne - vse v relativni rovine). Takze asi takto ...

Budu uvazovat konecny soucet

$S_n(x):=1+x+x^2+\cdots x^n,\qquad n\in\mathbb{N}_0,\: x\in\mathbb{R}$

O tomto je znamo, ze se da vyjadrit pro 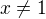$x\neq 1$ ve tvaru

$S_n(x)=\frac{1-x^{n+1}}{1-x}, n\in\mathbb{N}_0.$

Nastane-li vylouceny pripad, tj. $x=1$ , pak mame jiste snadno

$S_n(x)=1+1^2+\cdots +1^n=n+1.$

Tento pripad je snadny a z nasich uvah jej vyloucime. Podobne lze vylouct z techto uvah bod x=0 (drobnosti prenechavam ctenari).

Dale budeme derivovat funkci $S_n(x)$ vzhledem k promenne x. To dava v podstate dvoji vysledek:
(i)
$S_n'(x)=(1+x+x^2+\cdots x^n)'=0+1+2x+\cdots +nx^{n-1}=1+2x+\cdots +nx^{n-1}.$

(ii) Na druhou stranu plati ale vyse uvedena formule $S_n(x)=\frac{1-x^{n+1}}{1-x}$ . Derivace prave strany dava
$S_n'(x)=\left (\frac{1-x^{n+1}}{1-x}\right )'=\frac{-(n+1)x^n(1-x)-(1-x^{n+1})\cdot (-1)}{(1-x)^2}.$

Srovnanim derivace v (i) a (ii) pak je

$1+2x+\cdots +nx^{n-1}=\frac{-(n+1)x^n(1-x)-(1-x^{n+1})\cdot (-1)}{(1-x)^2}.$

Leva strana se pak zjednodusene zapisuje jako

$1+2x+\cdots +nx^{n-1}=\sum_{k=1}^{n}kx^{k-1}.$

Tazateli se jedna o nekonecno radu

$1+2x+\cdots +kx^{k-1}+\cdots =\sum_{k=1}^{\infty}kx^{k-1}=\lim_{n\to\infty}\sum_{k=1}^{n}kx^{k-1}=\nl =\lim_{n\to\infty}\frac{-(n+1)x^n(1-x)-(1-x^{n+1})\cdot (-1)}{(1-x)^2}.$

Bereme-li vsak v uvahu pouze takova realna cisla x, ze plati $x\in (-1,1)$ , vime, ze plati vztahy
$\lim_{n\to\infty}x^n=0=\lim_{n\to\infty}nx^n.$

Odtud tedy pro takovato realna cisla x
$1+2x+\cdots +kx^{k-1}+\cdots =\frac{1}{(1-x)^2},\quad x\in (-1,1).$

Drive vylouceny pripad x=0 je zahrnut vyse (je vsak trivialni). Pripad x=1 je jasny, dava totiz divergenci studovane nkonecne rady (drobnosti nechavam pro zajmece). Obdobne nepochodime prilis v pripade x=-1.

Poznamka. Uvedeny postup se lisi od vyse uvedeneho v tom, ze nepouziva pojmy stejnomerne konvergence, ale pojmu parcialni soucet nekonecne rady a nekterych znamych identit u limit. Zajemci necht si sami vyberou ten postup, ktery je pro ne vhodnejsi.