Matematické Fórum

pololilo · 04. 06. 2011 17:32

Zdravím všechny řešitelé matematiky a také ty co se tzv. usilovně připravují na přijímačky na VŠE :-)

Tady jsem narazil na jeden příklad, ale nevím si rady s tím znamínkem 'krát' mezi a3xa4 ...

Snad tam žádný úpravy nebudou třeba, nebo ne?

Dana1 · 04. 06. 2011 17:37

↑ pololilo:

Myslím, že:

Všetky členy okrem $a_1$ vyjadriť pomocou $a_1$ a diferencie $d$

Potom riešiť rovnicu...

pololilo · 04. 06. 2011 17:44

↑ Dana1:

JJ, to jsem taky zkoušel, akorát že vycházelo a^2 a k tomu 3da1 + 2da1 + 6d^2 a tohle už je podle mě neřešitelný.

Dana1 · 04. 06. 2011 17:53

↑ pololilo:

Nevychádza. Ani nevyjde kvadratická rovnica. Ako si zapísal napríklad $a_7$ ?

pololilo · 04. 06. 2011 19:05

↑ Dana1:

tam jsem ani nedošel. Já mám akorát že (zkusim to nějak napsat) 2a1 + 6d = 22 , (a1+2d)x(a1+3d)=88 - a tady jsem to roznásobil a vyšlo to, co jsem napsal v předchozím příspěvku a^2 a k tomu 3da1 + 2da1 + 6d^2

Olin · 04. 06. 2011 19:18

Moc nechápu, co s tím děláš.

$2 a_1 + 6d &= 44\\ (a_1+2d)(a_1+3d) &= a_1^2 + 5a_1d + 6d^2 = 88$ .

Přímočarý postup - vyjádřit z první rovnice jednu neznámou a dosadit do druhé. Chytřejší postup - $a_1+3d = \tfrac 12 (2a_1 + 6d)$ , odkud $(a_1 + 2d) \cdot 22 = 88$ .

MartinK

↑ pololilo:zdravím :) zkus ty rovnice vyjádřit pomocí 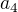$a_4$
pak ti vyjde $a_4 - 3d + a_4 + 3d=22\nl (a_4-d).a_4=88$
po úpravě $2a_4 =22; a_4=11$ dosadíš do druhé rovnice a vyjde ti $d=3$

pololilo · 04. 06. 2011 19:33

↑ Olin:

A jak pak získáš tu diferenci?

Dana1 · 04. 06. 2011 19:35

↑ pololilo:

Myslela som to podobne ako kolega Olin, ibaže nie tak chytře:

$2a1 + 6d = 22\\(a1+2d)\cdot (a1+3d)=88$ ,

z prvej rovnice:

$2a1 + 6d = 22\\ \color{red} a_1 = 11 - 3d$

dosadiť do druhej:

$(\color{red}11 - 3d\color{black}+2d)\cdot (\color{red}11 - 3d\color{black}+3d)=88$

Z toho:

$(11 - d)\cdot 11&=88 /:11\\11 - d &= 8$

MartinK · 04. 06. 2011 19:35

↑ pololilo:koukni se na můj postup výše :)

pololilo · 04. 06. 2011 19:43

↑ Dana1:

Jó jasně, ona je to dosazovačka. Dobrý už to vidim o:). Já myslel, že se to bude odčítat, kvůli eliminaci a1.
Tak Vám moc děkuju, moc mi to pomohlo a já jdu počítat dál. A dávam ++

↑ MartinK:

Ten je taky dobrej :D

Matematické Fórum

#1 04. 06. 2011 17:32

Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#2 04. 06. 2011 17:37

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#3 04. 06. 2011 17:44

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#4 04. 06. 2011 17:53

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#5 04. 06. 2011 19:05

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#6 04. 06. 2011 19:18

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#7 04. 06. 2011 19:26 — Editoval MartinK (04. 06. 2011 19:32)

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#8 04. 06. 2011 19:33

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#9 04. 06. 2011 19:35

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#10 04. 06. 2011 19:35

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

#11 04. 06. 2011 19:43

Re: Diference v aritmetické posloupnosti - násobení? (přijímačky VŠE)

Zápatí