Matematické Fórum

Taran · 05. 06. 2011 16:01

Pěkný den přeji,
v maturitní práci z matematiky jsem narazil na příklad, se kterým si doteď nevím rady.

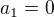Nekonečná posloupnost $(a_n)_{n=1}^{\infty}$ , kde $n \in N$ , je určena prvním členem $a_1 = 0$ a rekurentním vztahem: $a_{n+1} = q \cdot a_n + 4$

1) Učete všechny reálné hodnoty $q$ , pro něž je posloupnost $(a_n)_{n=1}^{\infty}$ konvergentní.

2) Pro $q = -\frac{1}{2}$ vypočtěte $\lim_{x\to \infty}a_n$

Bohužel se mi ani nepovedlo převést zadání posloupnosti z rekurentního do "klasického", takže jsem nemohl uplatnit mně známé postupy pro výpočet limity. A pro zjištění hodnot q tuším, že bych měl vyjít z definice limity, ale prakticky nevím, jak se do toho pustit. Poradí někdo?

Phate · 05. 06. 2011 16:31

A dokazal jsi vypsat prvnich par clenu, jak bylo zadani prvniho ukolu? Z toho to slo celkem pekne videt

Taran · 05. 06. 2011 17:30 — Editoval Taran (05. 06. 2011 17:44)

Ano, to jsem vyřešil, tak jsem tady dotyčný úkol ani neuváděl. První členy posloupnosti jsou po dosazení 0; 4; 2; 3; 2,5; 2,75;...
To mi ale k řešení ani jedné ze dvou úloh nepomohlo, i když jsem si jistý, že se to pouze nějakým triviálním způsobem převede do onoho vzorce pro n-tý člen. Jen to v tom stále nevidím.

Phate · 05. 06. 2011 17:34

↑ Taran:
vsak ty cleny nevycisluj, napis si je obecne

Taran · 05. 06. 2011 17:48

↑ Phate:
Teď nevím, jak moc obecně máš na mysli. Jestli pomocí paremetru q jako:
0, 4, 4q+4, 4q^2+4q+4, 4q^3+4q^2+4q+4
?

Phate · 05. 06. 2011 18:25

↑ Taran:
Ano, to mam na mysli. Nevidis v soucet nejake zname rady?

Taran · 05. 06. 2011 18:51

↑ Phate:
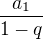Když jsi to zmínil, napadá mě, že bych na to mohl nahlížet jako na nekonečnou geometrickou řadu. Znamená to, že pak pro 1) musí platit podmínka $|q|<1$ a limitu spočítám jako $\frac{a_1}{1-q}$ ? Pokud bych za první člen posloupnosti místo nuly považoval 4, limita by vyšla 8/3, což by i odpovídalo číslu, ke kterému se posloupnost blíží, jak jsem vypsal výše.

MartinK

↑ Taran:
zdravím :)
takto jsem to řešil:

$a_1=0\nl a_2=4\nl a_3=4(q+1)\nl a_4=4(q^2+q+1)\nl a_5=4(q^3+q^2+q+1)$

V těch závorkách vidíš součet prvních n členů geometrické posloupnosti s prvním členem $a_1=1$ a koeficientem $k=q$ .

Všimni si ale, že pro každé n máš těch členů v závorce ne n ,ale n-1. Teď použiješ vzorec pro součet prvních n členů geometrické posloupnosti:

$S_{n-1}=a_1\cdot\frac{q^{n-1}-1}{q-1}$ $a_1=1$ proto jenom $S_{n-1}=\frac{q^{n-1}-1}{q-1}$

Teď už stačí napsat vzorec pro ntý člen: $a_n=4\cdot\frac{q^{n-1}-1}{q-1}$

Limita pro $q = -\frac{1}{2}$ mi pak vychází 0.

Phate · 05. 06. 2011 20:02 — Editoval Phate (05. 06. 2011 20:02)

↑ MartinK:

Limita pro $q = -\frac{1}{2}$ mi pak vychází 0.

Jakto?
$\lim_{n \to \infty}{4\cdot\frac{q^{n-1}-1}{q-1}}=4\frac{-1}{-\frac32}=\frac83$

MartinK · 05. 06. 2011 20:16

↑ Phate: Jo máš pravdu.

MartinK

↑ Taran:
Zdravím,
nebo mě taky napadlo, že neni potřeba vyvozovat vzorec pro ntý člen. Stačí si všimnout:

$a_n=4(q^{n-2}+q^{n-3}+....+q+1)$ a když dosadíme $\infty$ dostaneme

$a_\infty=4(q^{\infty-2}+q^{\infty-3}+....+q+1)$ to je vlastně nekonečná geometrická řada s prvním členem $a_1=1$ a koeficientem $k=q$ .

Použijeme proto vzorec pro součet nekonečné geometrické řady: 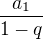$\frac{a_1}{1-q}$ . Ve výsledku potom pro $q = -\frac{1}{2}$ to vypadá následovně:

$a_\infty=4(\frac{1}{\frac{3}{2}})=\frac{8}{3}$

Taran · 06. 06. 2011 13:38

↑ MartinK: ↑ Phate:
Děkuji pánové, teď už to v tom vidím. :)

Rumburak · 06. 06. 2011 13:55

↑ MartinK:
Pouze s tím zápisem $a_\infty=4(q^{\infty-2}+q^{\infty-3}+....+q+1)$ opatrně.

Jak jsou podle Tebe definovány symboly $\infty - 2$ , $q^{\infty - 2}$ ? Co dostaneme, když do
$a_\infty=4(q^{\infty-2}+q^{\infty-3}+....+q+1)$ dosadíme $q = -\frac{1}{2}$ ?

MartinK · 06. 06. 2011 14:02

↑ Rumburak:

Vim, že to vypadá divně, ale nevěděl jsem jak to jinak zapsat :)

Rumburak · 06. 06. 2011 15:16

↑ MartinK:
Korektní zápis by byl (pokud jsem dobře pochopil Tvoji myšlenku)

$\lim_{n \to \infty} a_n =4 \sum_{k=0}^{\infty}q^k$ ,

pakliže bychom se chtěli vyhnout znaku sumy, napsali bychom

$\lim_{n \to \infty} a_n =4( 1 + q + q^2 + q^3 + ...)$ .

MartinK · 06. 06. 2011 15:19

↑ Rumburak:

Ano správně si pochopil :) a pěkně zapsáno.

Arminis · 06. 06. 2011 19:49

Pomozte mi prosím vyřešit tuto řadu, potřebuji rozhodnout zda-li je konvergentní nebo divergentní.
Děkuji.

Code:

(2x^n)/((2*n+1)^2*3^(n/2))

Phate · 06. 06. 2011 20:06

↑ Arminis:
zaloz si vlastni tema, prosim

Matematické Fórum

#1 05. 06. 2011 16:01

Posloupnost - hledání limity

#2 05. 06. 2011 16:31

Re: Posloupnost - hledání limity

#3 05. 06. 2011 17:30 — Editoval Taran (05. 06. 2011 17:44)

Re: Posloupnost - hledání limity

#4 05. 06. 2011 17:34

Re: Posloupnost - hledání limity

#5 05. 06. 2011 17:48

Re: Posloupnost - hledání limity

#6 05. 06. 2011 18:25

Re: Posloupnost - hledání limity

#7 05. 06. 2011 18:51

Re: Posloupnost - hledání limity

#8 05. 06. 2011 19:20 — Editoval MartinK (05. 06. 2011 19:45)

Re: Posloupnost - hledání limity

#9 05. 06. 2011 20:02 — Editoval Phate (05. 06. 2011 20:02)

Re: Posloupnost - hledání limity

#10 05. 06. 2011 20:16

Re: Posloupnost - hledání limity

#11 06. 06. 2011 13:25 — Editoval MartinK (06. 06. 2011 13:28)

Re: Posloupnost - hledání limity

#12 06. 06. 2011 13:38

Re: Posloupnost - hledání limity

#13 06. 06. 2011 13:55

Re: Posloupnost - hledání limity

#14 06. 06. 2011 14:02

Re: Posloupnost - hledání limity

#15 06. 06. 2011 15:16

Re: Posloupnost - hledání limity

#16 06. 06. 2011 15:19

Re: Posloupnost - hledání limity

#17 06. 06. 2011 19:49

Re: Posloupnost - hledání limity

Code:

#18 06. 06. 2011 20:06

Re: Posloupnost - hledání limity

Zápatí