Matematické Fórum

r2d2 · 07. 06. 2011 15:02

zdravím,
mám jen takovou malou otázku:
definičním oborem funkce $tg(x)$ je $\{\frac{\pi}{2} + \frac{k}{\pi}\}$ . Jaký je ale definiční obor funkce $-tg(x)$ ?
mám tušení, ale jen si to chci projistotu ověřit a nikde jsem to nenašel. asi mi tyhle informace nějak unikly:-)
děkuji

MartinK · 07. 06. 2011 15:07

↑ r2d2:
Nakresli si graf těch funkcí.

standyk

↑ r2d2:

Nesprávne si napísal aj 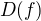$D(f)$ tangensu pretože to má byť $\mathrm{R} -\{\frac{\pi}{2} + {k}\color{red} \cdot{\pi} \color{black}\}$
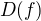
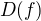A čo sa týka $D(f)$ $-tg(x)$ tak bude rovnaký ako $tg(x)$ pretože sa pri každej funkčnej hodnote zmení iba znamienko ale $D(f)$ ostáva
Na grafe to vyzerá nasledovne (modrá je $tg(x)$ a červená $-tg(x)$ a zvislé čiary sú asymptoty $\{\frac{\pi}{2} + {k}\color{red} \cdot{\pi} \color{black}\}$ )

r2d2 · 07. 06. 2011 15:12

↑ MartinK:to jsem samozřejmě udělal. mě by připadalo logické kdyby tg(x) i -tg(x) mělo stejný definiční obor, ale zjevně tomu tak není. Takže raději se vyslovím. je to tak že $-tg(x)$ má df $\{-\frac{\pi}{2} + \frac{k}{\pi}\}$ ??

MartinK

↑ r2d2:
Je to, jak psal výše ↑ standyk:.

r2d2 · 07. 06. 2011 15:18

↑ standyk:díky moc.
Jednak to pi/k je omyl, nějak mi to ujelo.
A co se týče toho oboru, uff, takže logika zůstává a vyhrává - MAJÍ STEJNÝ DEFINIČNÍ OBOR, pak ale nechápu kde mají chybu. Mám tady dva příklady kde jsem potřeboval určit definiční obory a vycházely by mi jedině tehdy, kdyby tg(x) měl jiný definiční obor než -tg(x). Tak jsem začal váhat jestli mají stejný definiční obor. Tak buď je tam chyba a nebo, což je pravděpodobnější mi tam něco uniklo. Jdu se tedy na to ještě podívat. díky moc

Matematické Fórum

#1 07. 06. 2011 15:02

definiční obor tangensu

#2 07. 06. 2011 15:07

Re: definiční obor tangensu

#3 07. 06. 2011 15:10 — Editoval standyk (07. 06. 2011 15:13)

Re: definiční obor tangensu

#4 07. 06. 2011 15:12

Re: definiční obor tangensu

#5 07. 06. 2011 15:17 — Editoval MartinK (07. 06. 2011 15:18)

Re: definiční obor tangensu

#6 07. 06. 2011 15:18

Re: definiční obor tangensu

Zápatí