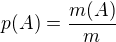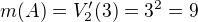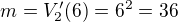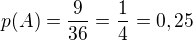Matematické Fórum

↑ zdenek1:
přesně tak :) totiž počet příznivých výsledků je 9 a počet všech možností je 36.

Ahoj,

já v té pravděpodobnosti moc nevynikám, ale vyřešil bych to tak, že si spočtu, kolik je možností, že padnou lichá čísla, poté bych si udělal možnosti, že padnou jakákoliv dvě čísla.

Nevím, jak poradit více obecně... Vychází mi to jako Zděňkovi .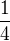 

Možná...

Celkový počet možností - zauvažuj nad tím tak, že máš dvě kostky, na kterých padají čísla od 1 do 6. Počet prvků by tedy (dle mého) měl být 6 a jednalo by se o variace s opakováním.

Na zbytek zkus přijít sám, avšak i počet lichých dvojic se spočte podobně.

Řešení napíšu skrytě, takže pokud to chceš spočíst, podívej se až pak:

Skrytý text:


Počet možností, že padnou liché dvojice (lichá čísla do šesti jsou tři - 1, 3, 5), tvoříme dvojice, můžeme opakovat čísla (3,3 je také lichá dvojice dvou kostek) a záleží nám na pořadí (1,3 je rozdíl oproti 3,1 - pokud rozlišujeme kostky). Proto



Celkový počet možností jsou dvojice všech čísel, jedná se tedy o stejný princip, jen se šesti prvky:



proto

Nebo:
Pravdepodobnost, ze mi na jedne kostce padne liche cislo je 0.5, protoze licha jsou na kostce tri cisla z 6. Kdyz takovou kostku pridame druhou, tak mame na obou z tech kostek 50% sanci na padnuti licheho cisla a potrebujeme, aby se tyto jevy staly zaraz, takze 0.5*0.5=0.25.

Zajimalo by me, jak byste secitali moznosti pro 10 kostek.

↑ Phate:

Ten můj postup by ale šel použít i na více kostek, nepletu se?

Počet kostek = k
počet stěn na kostce = n (celkové)
poloviční počet stěn na kostky = n (pro liché)
A vždy variace s opakováním

Je to správně? Sám si teď nejsem jist, pokud ne, asi bych raději skryl předchozí příspěvek, aby to žadatele nemátlo.