Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 06. 2011 20:29
Problém s odmocninami
Zdravím,
v pondělí dělám přijímačky na VŠ, tak jsem si pročítal nějaké vzorové z předchozích let a narazil jsem na tento příklad, u kterého jsem se naprosto zasekl:
Nechť a, b jsou kladná reálná čísla, pro která platí a>b. Výraz
se dá upravit na tvar:
a) a(a-b)
b) a-b
c) a+b
d) b-a
e) žádná z uvedených možností není správná
Nevíte prosím někdo, jak postupovat a jaký je správný výsledek?
Předem děkuji.
Offline
- (téma jako vyřešené označil(a) Dana1)
#2 10. 06. 2011 20:33 — Editoval BakyX (10. 06. 2011 21:13)
Re: Problém s odmocninami
Ahoj..Využi toto:

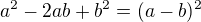
Pozri si http://wiki.matweb.cz/index.php/U%C5%BE … %A9_vzorce
1^6 - 2^6 + 3^6 = 666
Offline
#4 10. 06. 2011 21:10
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: Problém s odmocninami

skus začít tím, že si zavedeš substituci za  třeba
třeba
Offline
#6 10. 06. 2011 21:16 — Editoval Dana1 (10. 06. 2011 21:24)
- Dana1
- Host
Re: Problém s odmocninami
↑ VojtechSejkora:
1. Napísal si:
a teď si nejsem úplně jist, zdali to můžu umocnit:(
Myslím, že tu o žiadne umocňovanie nejde - ako napísal BakyX (zdravím), využíva sa "vzorec" 
2.: , rovnosť platí len niekedy. Treba sa presvedčiť, či zadané čísla a,b podmienku pre uvedené odmocnenie spĺňajú.
, rovnosť platí len niekedy. Treba sa presvedčiť, či zadané čísla a,b podmienku pre uvedené odmocnenie spĺňajú.


 a teď si nejsem úplně jist, zdali to můžu umocnit:(
a teď si nejsem úplně jist, zdali to můžu umocnit:(

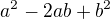 a to je již vzorec
a to je již vzorec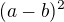 a jelikož jsem tam někde umocňoval tak bych nyní odmocnil a mám řešení
a jelikož jsem tam někde umocňoval tak bych nyní odmocnil a mám řešení
 bys dosadil
bys dosadil  to jisté s B a b a měl bys dojít ke stejnému výsledku (alespon doufám)
to jisté s B a b a měl bys dojít ke stejnému výsledku (alespon doufám) místo
místo  ?
?