Matematické Fórum

Alivendes · 14. 06. 2011 21:35

Příklad pro ↑↑ Martty:
Je dáno např:
$sin2x=\frac{4}{7}$ a máme vyjádřit tg x
$2x=a$
$sina=\frac{4}{7}$
$tga=\frac{sinx}{\sqrt{1-sin^2a}}$
$tga=\frac{\frac{4}{7}}{\sqrt{1-\frac{16}{49}}}$
$tga=\frac{\frac{4}{7}}{\frac{\sqrt33}{7}}=\frac{4}{\sqrt33}=\frac{4\sqrt33}{33}$
$tg2x=\frac{2tgx}{1-tg^2x}$
$\frac{4\sqrt33}{33}=\frac{2tgx}{1-tg^2x}$

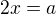
Vyjde kvadratická rovnice, kde získáš tgx

Martty · 14. 06. 2011 21:53

rozumim tomu až do teď pak se ztrácim ;)

$tga=\frac{\frac{4}{7}}{\frac{\sqrt33}{7}}=\frac{4}{\sqrt33}=\frac{4\sqrt33}{33}$

Alivendes

↑ Martty:
Vypočítali jsme, že:
$tga=\frac{\frac{4}{7}}{\frac{\sqrt33}{7}}=\frac{4}{\sqrt33}=\frac{4\sqrt33}{33}$
ale!
$a=2x$
$tga=tg2x$
Teď se musí dosadit do vzorce pro tg dvojnásobného úhlu:
$tg2x=\frac{2tgx}{1-tg^2x}$
$\frac{4\sqrt33}{33}=\frac{2tgx}{1-tg^2x}$

Ted už stačí jen dopočítat tangens:
$\frac{4\sqrt33}{33}(1-tg^2x)-2tgx=0$
$S:tgx=t$
$\frac{4\sqrt33}{33}(1-t^2)-2t=0$

Takhle dopočítáš tgx
Je to přehlednější ?

Martty · 14. 06. 2011 22:19

↑ Alivendes:
ano, je to přehlednější
takto se tedy postupuje vždy?! ale ten příklad přdtím byl jednodušší ;)

Alivendes · 14. 06. 2011 22:41

↑ Martty:
No dobře tak ale když máš zadaný úhel 90° tak fakt není co řešit ...

Martty · 14. 06. 2011 22:57

↑ Alivendes:

jasný to chápu, když to je význačná hodnota ...
já bych právě ani na začátku nezaváděl tu substituci, ale pak jsem se nehnul z místa nebo se točil stále v kruhu ;)

a dotaz pro fci gotangens by se to pouze otočilo a postup by byl stejný že ano.... nebo by se pak výsledek dal vy jádřit jako $cotga=\frac{1}{tgx}$
$cotga=\frac{\sqrt{1-sin^2a}}{sinx}$

Děkuji jinak za názorné vysvětlení ;)

Alivendes · 14. 06. 2011 23:00

↑ Martty:'
:o) ano, to se dá odvodit i takto:
$cotgx=\frac{cosx}{sinx}=\frac{\sqrt{1-sin^2x}}{sinx}$

Martty · 14. 06. 2011 23:08

↑ Alivendes:

a mohl bys mi ještě prosím napsat jak by to vypadalo pro
$cotg2x=?$
když $tg2x=\frac{2tgx}{1-tg^2x}$
Již nebudu otravovat Děkuji :)

Alivendes · 14. 06. 2011 23:10

↑ Martty:
Tak chvilku, musím to odvodit, nepamatuju si to.

Alivendes

Tady to mám:
$cotg(\alpha\pm\beta)=\frac{cotg\alpha.cotg\beta\mp1}{cotg\alpha\pm cotg\beta}$
Takže pro náš úhel:
$cotg(x+x)=\frac{cotg^2x-1}{2cotgx}$

Martty · 14. 06. 2011 23:20

↑ Alivendes:

jéé, Děkuji mockrát .... snad jen už aby se tento příklad objevil u přijímaček :)
Goniometrie je pro mě jedna velká španělská vesnice ;)

Alivendes · 14. 06. 2011 23:23

↑ Martty:
Není zač :), děláš teď přijímačky na vysokou školu ?

Kdyžtak třeba na wikipedii je celkem přehledný seznam všech možných vozrečků na goniometrické funkce. Stačí zadat goniometrické funkce.

Martty · 14. 06. 2011 23:29

↑ Alivendes:

ano, na vysokou. Bohužel tabulky ani kalkulačka není povolená. Tak se trochu bojim, že ve stresu udělám chybu a bude to ...
Dobře Děkuji, zítra dorazím goniometrii a hurá na Analytiku! :D :)
(zlatý rovnice s parametrem, logaritmy a jiné) :)

Alivendes · 14. 06. 2011 23:41

↑ Martty:'
Tak to přeji hodně štěstí :) ...není to těžké, akorát všechno tu souvisí se vším ...je dobré naučit se alepson pár vzorečků.

zdenek1 · 14. 06. 2011 23:49

↑ Alivendes:
A co takto:
$\sin2x=\frac47$
$2\sin x\cos x=\frac47$
$\sin x \cos x=\frac27\qquad|:\cos^2x$
$7\tan x=2\frac1{\cos^2x}=2(1+\tan^2x)$
$2\tan^2x-7\tan x+2=0$

Alivendes · 14. 06. 2011 23:51

↑ zdenek1:
Tušil jsem, že existuje i lepší cesta, ale nějak mě nic nenapadlo, nejšpíš proto, že vzorec který si použil moc nepoužívám, každopádně děkuji.

Matematické Fórum

#1 14. 06. 2011 21:35

Goniometrické funkce

#2 14. 06. 2011 21:53

Re: Goniometrické funkce

#3 14. 06. 2011 21:58 — Editoval Alivendes (14. 06. 2011 21:59)

Re: Goniometrické funkce

#4 14. 06. 2011 22:19

Re: Goniometrické funkce

#5 14. 06. 2011 22:41

Re: Goniometrické funkce

#6 14. 06. 2011 22:57

Re: Goniometrické funkce

#7 14. 06. 2011 23:00

Re: Goniometrické funkce

#8 14. 06. 2011 23:08

Re: Goniometrické funkce

#9 14. 06. 2011 23:10

Re: Goniometrické funkce

#10 14. 06. 2011 23:14 — Editoval Alivendes (14. 06. 2011 23:14)

Re: Goniometrické funkce

#11 14. 06. 2011 23:20

Re: Goniometrické funkce

#12 14. 06. 2011 23:23

Re: Goniometrické funkce

#13 14. 06. 2011 23:29

Re: Goniometrické funkce

#14 14. 06. 2011 23:41

Re: Goniometrické funkce

#15 14. 06. 2011 23:49

Re: Goniometrické funkce

#16 14. 06. 2011 23:51

Re: Goniometrické funkce

Zápatí