Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 06. 2011 15:50
Komplexní čísla-moivreova věta
Snažím se spočítat následující příklad, ale jelikož jsem matematiku už dlouho neviděla mám značné mezery. Budu vděčná za jakoukoli pomoc (jen prosím o "polopatistické" vysvětlení).
Vypočítat se má imaginární část komplexního čísla.
z=(-1+i)^ 15
Vyjít to má 2^-7
Offline
- (téma jako vyřešené označil(a) Kei)
#3 16. 06. 2011 16:02 — Editoval Kei (16. 06. 2011 16:05)
Re: Komplexní čísla-moivreova věta
↑ standyk:
Převádění na goniometrický tvar se mi většinou podaří, mělo by to být i po umocnění sqrt2^15*(cos15*3/4π+i sin 15*3/4π)
Největší kámen úrazu jsou v tomhle pro mě operace se sinem a cosinem, takže nevím co s tím dál (za předpokladu že to mám vůbec dobře).
Offline
#4 16. 06. 2011 16:14 — Editoval standyk (16. 06. 2011 16:17)
Re: Komplexní čísla-moivreova věta
↑ Kei:
Áno správne: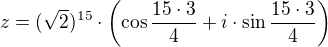
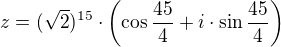
Goniometrické funkcie  a
a  majú periódu
majú periódu  preto tie zlomky môžeme upraviť nasledovne:
preto tie zlomky môžeme upraviť nasledovne:![kopírovat do textarea $z=(\sqrt2)^{15} \cdot \[cos\({\color{red}\frac{40}{4}\pi\color{black} + \frac{5}{4}\pi}\)+i \cdot \sin\({\color{red}\frac{40}{4}\pi \color{black}+ \frac{5}{4}\pi}\)\]$](/mathtex/5e/5ee92469d8ff50fa6355d0ef3d2fdc6a.gif)
To čo je označené červenou je tá perióda  - násobok dvojky.Preto to môžeme vynechať, lebo výsledok to nezmení. Preto:
- násobok dvojky.Preto to môžeme vynechať, lebo výsledok to nezmení. Preto: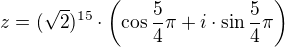
Teraz preveď to posledné vyjadrenie späť na algebraický tvar aby si mohla určiť imaginárnu časť tohto komplexného čísla.
Offline
#5 16. 06. 2011 16:18
#6 17. 06. 2011 14:01
Re: Komplexní čísla-moivreova věta
↑ standyk: když chceme vypočítat reálnou a imaginární část čísla vychází to v záporné hodnotě, když je to ve 3. kvadrantu?
Offline
#8 17. 06. 2011 14:19
Re: Komplexní čísla-moivreova věta
↑ standyk: protože jsem počítala (odmocnina ze 2/2 - i odmocnina ze 2/2)ˇ49
při výpočtu 3pí/4 x 45 = pí/4 a nebo 5pí/4 ?
kdyby to bylo 5pí/4 tak by to byl 3.kvadrant kde je sin i cos záporný, ale reálná část má vyjít kladná (odmonina ze 2/2)
Poradil by jsi mi prosím?
Offline

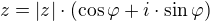

 aj
aj  záporný, takže áno.
záporný, takže áno.