Matematické Fórum

Mathe · 18. 06. 2011 17:40

Ahoj, měl bych pár dotazů ohledně příkladů do logiky:

1. Existuje ekvivalence taková, že jediná třída ekvivalence obsahuje celou množinu M ?
Nějak ani nevím co se po mě chce, třída ekvivalence relace R z AxB je $R[a] = {b \epsilon A | a R b }$ .

2. Nějak mi není jasné, jak lze převést do CNF výraz $\varphi = (P \wedge Q) \vee (R \wedge S)$ . Vím pouze, jak rozložit výraz $\varphi = P \vee (R \wedge S) \equiv (P \vee R) \wedge (P \vee S)$

Děkuji za pomoc.

Wotton · 18. 06. 2011 17:51

1: třída ekvivalence je třída prvků ekvivalentních (ve smyslu dané ekvivalence) s daným prvkem. Takže taková ekvivalence existuje, je to relace ve které jsou všechny prvky se všemi prvky.

2: stačí provést distributivitu pro dvě závorky (zkus si vzpomenout na násobení mnohočlenu mnohočlenem, princip je úplně stejný)

Mathe · 18. 06. 2011 19:12

1. Jestli jsem to pochopil správně, tak by to musela být relace R, která by množinu přirozených čísel zobrazila na celou množinu celých čísel.
Relace R je definována jako $R \subset A \times B$ čili $A \equiv \Bbb N$ a stejně tak i B.
Ale nevím, jaká funkce by to splnila (často dostáváme relace typu = <= >=) tak jestli by šla tato relace nějak popsat.

2. Takže z toho vznikne toto: $(P \wedge R) \vee (P \wedge S) \vee (Q \wedge R) \vee (Q \wedge S)$

Děkuji

Oxyd · 18. 06. 2011 19:27

↑ Mathe:

1) Terminologická poznámka: Relace a funkce jsou dva podobné, avšak odlišné pojmy. Funkce je speciální případ relace, ale ne každá relace je funkce. Speciálně uspořádání jako <, <= apod. nejsou funkce.

Navíc relace z A do B se většinou definuje jako libovolná nevlastní podmnožina A x B -- symbolicky: $R \subseteq A \times B$ . Konkrétně smí být $R = A \times B$ . Což je přesně ta relace, kterou ti Wotton nabídl (tedy zřejmě $R = M \times M$ ). Teď bys ještě měl ověřit, že to je ekvivalence a že má právě jedinou třídu ekvivalence, a to celou M.

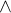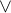2) Asi to máš správně. Jen jsi prohodil symboly $\wedge$ a $\vee$ . Mělo by to být $(P \vee R) \wedge (P \vee S) \wedge (Q \vee R) \wedge (Q \vee S)$ .