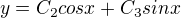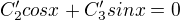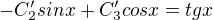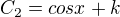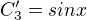Matematické Fórum

vysoka · 19. 06. 2011 21:50 — Editoval vysoka (19. 06. 2011 21:55)

$y'''+y'=tgx$

viem ze je nedela vecer/ no ale co uz uloha je jasna ...
..takze mame trojnasobny korienok... :)
po uprave mame x=0 a dvojnasobny koren -1 ? ok ...

Alivendes

↑ vysoka:
Já ti dám diferenciální rovnici na zahřátí :D, je večer :D, pokusím se to vyřešit jako lineární diferenciální rovnici druhého řádu: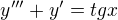
$y'''+y'=tgx$

char. rovnice: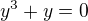
$y^3+y=0$
$y(y^2+1)=0$
$y_1=0$
$y_{23}=\pm i$

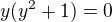
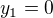
Obecné řešení: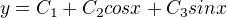
$y=C_1+C_2cosx+C_3sinx$

Může být ??

Doufám že nechceš úplné řešení

vysoka · 19. 06. 2011 22:16

↑ Alivendes:vsak to napisem do pisomky a mozno mi daju aj 100 % :)
len zistit ci neurcitych koeficientov metoda ci variacie konstant / wronskian ? v nej viem ze je univerzal...

vysoka · 19. 06. 2011 22:17 — Editoval vysoka (19. 06. 2011 22:18)

↑ Alivendes: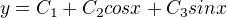 $y=C_1+C_2cosx+C_3sinx$ zderivujem ... a zostacim W , W_1 , W_2 ... integrujem ... moze byt ?
tusim ze som sa uz aj ja zahrial

Alivendes · 19. 06. 2011 22:20

↑ vysoka:
To je otázka, kdyby se to počítalo normálně, tak by vyšla soustava dvou rovnic pro tři neznámé, opravdu netuším, jak bych vymýšlel další pomínky.
Vycházel bych z toho, že je na první pohled vidět, že celá diferenciální rovnice platí pro $y=0$ proto bych počítal s první konstantou jako s nulou a dál to řešil jako diferenciální rovnici druhého řádu...

vysoka · 19. 06. 2011 22:46 — Editoval vysoka (19. 06. 2011 22:50)

↑ Alivendes:kedy by sa to pocitalo normalne ? uz ledva pozeram na obrazovku... sorry

Alivendes

↑ vysoka:
Dál bych to řešil takto, C1 položíme rovno nule, dsotáváme:
$y=C_2cosx+C_3sinx$

Podmínky:
$C_2' cosx+C_3'sinx=0$
$-C_2' sinx+C_3'cosx=tgx$

Vypočítáme přes wronskiány..

vysoka · 19. 06. 2011 22:49

Alivendes napsal(a):
↑ vysoka:
To je otázka, kdyby se to počítalo normálně,

Alivendes · 19. 06. 2011 22:51

↑ vysoka:
Kdybych to počítal normálně, musel bych do toho co jsem napsal, zahrnout ještě třetí proměnou, a to by nešlo spočítat...

vysoka · 19. 06. 2011 22:57

↑ Alivendes:aha ok ... takze s tymi W .. to bol dobry napad :) mozem veselo ist odfukovat ... a zajtra zhodnotit situaciu ...:) diky v tomto stave uz nie som schopnz si to napisat na papier...good night

Alivendes · 19. 06. 2011 22:58

↑ vysoka:
Já to sem napíšu, chvilku strpení:

maly_kaja_hajnejch-Lazov · 19. 06. 2011 22:59

Variace konstant se da delat i pro rovnice tretiho radu, ale jinak, nez je vyse. Vyjdou tri rovnice o trech neznamych, je to popsano v literature tak je asi zbytecne to sem nejak rozepisovat.

K te puvodni rovnici:

Substituce y'=z to prevede na rovnici

z''+z=tg(x)

Potom to vyresim variaci konstant (viz napriklad MAW) a vysledek zintegruju abych ze z(x) dostal y(x).

maly_kaja_hajnejch-Lazov · 19. 06. 2011 23:01

Alivendes napsal(a):
↑ vysoka:
Vycházel bych z toho, že je na první pohled vidět, že celá diferenciální rovnice platí pro $y=0$ proto bych počítal s první konstantou jako s nulou a dál to řešil jako diferenciální rovnici druhého řádu...

Pro y=0 mame rovnici 0=tg(x), ktera rozhodne neplati na zadnem otevrenem intervalu. Takze y=0 neni resenim, bohuzel ....

maly_kaja_hajnejch-Lazov · 19. 06. 2011 23:05

↑ Alivendes: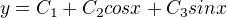 $y=C_1+C_2cosx+C_3sinx$ -- tohle bohuzel neni obecne reseni, jak pisete. Je to obecne reseni asociovane homogenni rovnice. Pokud za slova "obecne reseni" nepridam zadny dovetek, tak se samo sebou rozumi reseni puvodniho problemu, coz v tomto pripade neplati.

Omlouvam se, ze jsem sem tak vpadl, po dlouhe dobe jsem sem zavital a nejak jsem neudrzel prsty :)
Verim, ze dal se vam to podari spocitat, doporucuji potom overit u wolframu aplha.

Alivendes · 19. 06. 2011 23:06

$C_2' cosx+C_3'sinx=0$
$-C_2' sinx+C_3'cosx=tgx$
$D=1$
$D_{C_2'}=-sinx$
$D_{C_3'}=sinx$

$C_2'=-sinx$
$C_2=cosx+k$

$C_3'=sinx$
$C_3=-cosx+k$

Dosadíme do naší rovnice:
$y=C_1+C_2cosx+C_3sinx$

Konec ...ale neručím za to, že se takto dá počítat diferenciální rovnice třetího stupně, prosím o kontrolu

Alivendes · 19. 06. 2011 23:07

↑ maly_kaja_hajnejch-Lazov:

:) v pořádku, zajímá mě, jak se to dá počítat ...tak uvedte prosím vlastní postup

Alivendes

↑ maly_kaja_hajnejch-Lazov:

Proč mě sakra nenapadla ta substituce, jsem já to ale idiot , to, co jsem spočetl výše, je to, co vyjde po substituci 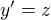$y'=z$

Mnohokrát Vám děkuji.

maly_kaja_hajnejch-Lazov

↑ Alivendes: Muj postup je v prispevku cislo #12: prevedeni na rovnici druheho radu a s tim si uz treba tazatel poradi. Pokud ne, doporucuji mu MAW a pokud ani to ne, tak at sem prosim posle dotaz.

btw: Zkouska napovi, ze soustavu pro C'_2 a C'_3 mate bohuzel vyresenu spatne, jeden z integralu bude mnohem hnusnejsi.

vysoka · 20. 06. 2011 07:56 — Editoval vysoka (20. 06. 2011 08:12)

↑ maly_kaja_hajnejch-Lazov:↑ Alivendes:Dakujem obom neviem ci to pojde skusil som to dat do MAW http://wood.mendelu.cz/math/maw/lde2/ld … ko=Odeslat
... len potom na konci sa asi neyabudnut vratit k povodnej premennej

vysoka · 20. 06. 2011 22:11

mozem oznacit ako vyriesene ak nie su ziadne namietky ??? :) chcem mat sladke sny

jelena · 26. 06. 2011 00:42

vysoka napsal(a):
mozem oznacit ako vyriesene ak nie su ziadne namietky ??? :) chcem mat sladke sny

to bys mohl, další také, děkuji

Matematické Fórum

#1 19. 06. 2011 21:50 — Editoval vysoka (19. 06. 2011 21:55)

diferencialna rovnica na zahriatie

#2 19. 06. 2011 21:59 — Editoval Alivendes (19. 06. 2011 22:11)

Re: diferencialna rovnica na zahriatie

#3 19. 06. 2011 22:16

Re: diferencialna rovnica na zahriatie

#4 19. 06. 2011 22:17 — Editoval vysoka (19. 06. 2011 22:18)

Re: diferencialna rovnica na zahriatie

#5 19. 06. 2011 22:20

Re: diferencialna rovnica na zahriatie

#6 19. 06. 2011 22:46 — Editoval vysoka (19. 06. 2011 22:50)

Re: diferencialna rovnica na zahriatie

#7 19. 06. 2011 22:49 — Editoval Alivendes (19. 06. 2011 22:58)

Re: diferencialna rovnica na zahriatie

#8 19. 06. 2011 22:49

Re: diferencialna rovnica na zahriatie

Alivendes napsal(a):

#9 19. 06. 2011 22:51

Re: diferencialna rovnica na zahriatie

#10 19. 06. 2011 22:57

Re: diferencialna rovnica na zahriatie

#11 19. 06. 2011 22:58

Re: diferencialna rovnica na zahriatie

#12 19. 06. 2011 22:59

Re: diferencialna rovnica na zahriatie

#13 19. 06. 2011 23:01

Re: diferencialna rovnica na zahriatie

Alivendes napsal(a):

#14 19. 06. 2011 23:05

Re: diferencialna rovnica na zahriatie

#15 19. 06. 2011 23:06

Re: diferencialna rovnica na zahriatie

#16 19. 06. 2011 23:07

Re: diferencialna rovnica na zahriatie

#17 19. 06. 2011 23:10 — Editoval Alivendes (19. 06. 2011 23:11)

Re: diferencialna rovnica na zahriatie

#18 19. 06. 2011 23:12 — Editoval maly_kaja_hajnejch-Lazov (19. 06. 2011 23:12)

Re: diferencialna rovnica na zahriatie

#19 20. 06. 2011 07:56 — Editoval vysoka (20. 06. 2011 08:12)

Re: diferencialna rovnica na zahriatie

#20 20. 06. 2011 22:11

Re: diferencialna rovnica na zahriatie

#21 26. 06. 2011 00:42

Re: diferencialna rovnica na zahriatie

vysoka napsal(a):

Zápatí