Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 06. 2011 18:32
Rovnice - počet jejich řešení
Dobrý den,
stále mi tento příklad nevychází podle uvedeného výsledku:
Počet všech reálných řešení rovnice je? (1)
Vychází mi x_1 = 10 a x_2 = 2 , kde vycházím z podmínky x je větší nebo rovno -5/2 .
Děkuji za radu.
Offline
- (téma jako vyřešené označil(a) joinusman)
#2 21. 06. 2011 18:42 — Editoval standyk (21. 06. 2011 18:43)
Re: Rovnice - počet jejich řešení
↑ joinusman:
Výsledok odmocnenia môže byť z definície len nezáporné číslo. Preto vypadáva ten koreň  . Keby si dosadil 2 za x dostaneš na pravej strane
. Keby si dosadil 2 za x dostaneš na pravej strane  a to by už nesedelo z definíciou odmocniny. Skutočne má teda len 1 koreň a to:
a to by už nesedelo z definíciou odmocniny. Skutočne má teda len 1 koreň a to: 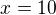
Offline
#3 21. 06. 2011 18:49
- janca361

- .
- Příspěvky: 3284
Re: Rovnice - počet jejich řešení
↑ joinusman:
Musíš pracovat se zkouškou (v tomto případě jednodušší) nebo podmínkami řešitelnosti, protože umocnění obou stran rovnice není ekvivalentní úprava.
Když povedeš zkoušku vypadne ti kořen  a zůstane ti jen
a zůstane ti jen  , které je řešení rovnice. Proto má tato rovnice jen jedno řešení.
, které je řešení rovnice. Proto má tato rovnice jen jedno řešení.
Offline
