Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 06. 2011 18:12 — Editoval TehTox (19. 06. 2011 18:32)
Re: příklad
No, Jelikož přímka náleží elipse (je její tečnou), co z toho vyplývá? Zkus na to přijít sám ...
Edit: při výpočtu jsem se do toho nějak zamotal. Může mi někdo objasnit co je špatně? Moje řešení je skryté níže.
Offline
#3 19. 06. 2011 20:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: příklad
↑ TehTox:
Zdravím,
myslím, že v pořádku, až na nějakou nepozornost pří úpravě.


 , podmínkou má být, že D=0, aby přímka byla tečnou. Z toho 2 hodnoty parametru m. Tedy ještě řešení rovnice D=0.
, podmínkou má být, že D=0, aby přímka byla tečnou. Z toho 2 hodnoty parametru m. Tedy ještě řešení rovnice D=0.
V pořádku? Děkuji.
Offline


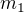 a
a 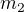 , které, po vypočtení, spolu vynásobíš a máš řešení.
, které, po vypočtení, spolu vynásobíš a máš řešení.





 , což je podle Vietových vztahů
, což je podle Vietových vztahů 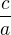 po úpravě rovnice
po úpravě rovnice