Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 06. 2011 04:40
- stuart clark

- Příspěvky: 1015
- Reputace: 7
max. min.
If  .Then find Maximum and Minimum value of
.Then find Maximum and Minimum value of 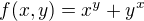
Offline
- (téma jako vyřešené označil(a) byk7)
#2 21. 06. 2011 10:19
Re: max. min.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 22. 06. 2011 09:30
#4 22. 06. 2011 21:53
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: max. min.
↑ Pavel:
Can values of f really be as close to 0 and 2 as needed? When choosing e.g. x,y so that x^y is "as close as needed" to 1, can it really be so that y^x can also be close to 1? .... eg. for x=0.999, y=0.001 x^y really is close to 1 but for such choice y^x is definitely not close to 1....
"Máte úhel beta." "No to nemám."
Offline
#5 22. 06. 2011 22:41 — Editoval Pavel (22. 06. 2011 22:42)
Re: max. min.
If you set 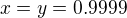 then
then 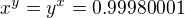 . You took
. You took  and
and  such that
such that 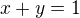 . However, it is not required in your problem. The only condition for
. However, it is not required in your problem. The only condition for  and
and  is
is  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 23. 06. 2011 20:17
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: max. min.
↑ Pavel:
Of course, Thanks. But how can I approach "as close as I want" to 0?...
"Máte úhel beta." "No to nemám."
Offline
#7 07. 07. 2011 18:31
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: max. min.
In fact, my hypothesis is that the infimum of the values of f is not 0 but 1.
"Máte úhel beta." "No to nemám."
Offline
 ,
, .
. does not exist. There is only the infimum resp. supremum of
does not exist. There is only the infimum resp. supremum of ![kopírovat do textarea $M=\{[x,y]\in\mathbb R^2;0<x,y<1\}$](/mathtex/1a/1a26a35a892080fd151528291ee06c55.gif) . In other words, for every
. In other words, for every  there exists
there exists ![kopírovat do textarea $[x_0,y_0]\in M$](/mathtex/6c/6c9f3385b8689eae9cce435a1aab3063.gif) such that
such that  resp.
resp.  but on the other hand there does not exist any
but on the other hand there does not exist any ![kopírovat do textarea $[x,y]\in M$](/mathtex/ac/ac646e26da3500dce549f365f20d7325.gif) such that
such that 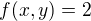 resp.
resp. 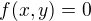 .
.