Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 06. 2011 19:33
- check_drummer

- Příspěvky: 4629
- Reputace: 99
Re: Rovnosť polynómov
Napadá mě - 0,1, x^n (položením y=F(x) získáme F(y)=y^n).
"Máte úhel beta." "No to nemám."
Offline
#3 23. 06. 2011 14:43
Re: Rovnosť polynómov
Na začiatok..Nech stupeň polynómu F(x) je "k". Stupeň F(F(x)) je k^2. Stupeň (F(x))^n je kn. Je teda zrejmé, že k=n. Skúsim teraz použiť ten postup podobný príkladu 3.7 http://imageshack.us/photo/my-images/148/beznzvuxb.png/
Nech "l" označuje index najvyššieho koeficientu, ktorý sa nerovná 0 (l < n). Rovnosť prepíšeme potom ako:
Porovnánim koeficientov pri 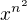 hneď vidíme, že
hneď vidíme, že 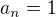 . Trošku sa to potom vykráti a ostane:
. Trošku sa to potom vykráti a ostane: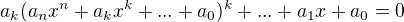
TO vyzerá celkom pekne, ale keďže na pravej strane máme nulový mnohočlen, tak zrejme F(x) je nulový (čo je jedno riešenie) alebo a_k=0, čo je spor s predpokladom.
Polynóm F(x) je teda v tvare 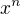
1^6 - 2^6 + 3^6 = 666
Offline

