Matematické Fórum

lucik.kicul · 25. 06. 2011 13:19

Dobrý den,
potřebovala bych pomoci s řešením těchto dvou příkladů, zdají se mi lehké a štve mě, že se nemůžu dobrat ke správnému výsledku =(.
Zadání: integrály vypočtěte užitím rozkladu na parciální zlomky.
1. Int x/x+5 dx- u tohoto příkladu má vyjít výsledek: x- 5ln|x+5|+C
Moje řešení: vytkla jsem si x a počítala jsem Int 1/x+5 potom jsem si vytkla 1/5 a počítala: x*1/5* int 1/x= x-5.ln|x+5|+C
mám ten postup vůbec dobře, když jsem nepoužila parciální zlomek? Neměla jsem tam použít substituci za x+5? Mě tam hlavně mate to x/x+5, kdyby tam bylo 3/x+5, tak to bych uměla

2.Int 3x-1/x+2 dx: výsledek má vyjít 3x-7ln|x+2|+C
a tady nevím, jak dále postupovat
Děkuji

halogan · 25. 06. 2011 13:30

1. Co kdybyste v čitateli přičetla a odečetla pětku? To už byste uměla pak řešit, ne?

2. To se řeší podobně, ale nejprve doděláme jedničku.

Alivendes

Ahoj:)
Dáme každý příklad do samostantého tématu:

$\int \frac{x}{x+5}dx=x.ln|x+5|-\int (x)'ln|x+5|=x.ln|x+5|-\int ln|x+5|= \nl x.ln|x+5|-(x+5).ln|x+5|+(x+5)= ln|x+5|(x-(x+5))+(x+5)=x+5-5.ln|x+5|+C$

halogan

Ještě vsuvka — i když je postup od ↑ Alivendes: formálně víceméně správně (a trochu porušuje pravidla :-), zkus to napřed tak, jak píši já. Nepotřebuješ pak vůbec per partes, jen využiješ toho, že

$\int \frac{f'(x)}{f(x)}\,\mathrm{d}x = \log |f(x)| + C$
(nějaké podmínky tam jsou, ty teď vynechám)

a toho, že derivace lineární funkce je jen ta konstanta před $x$ .

Tento postup ale asi znáš, podle tvého úvodního příspěvku, kde píšeš, že to již problém není.

Alivendes · 25. 06. 2011 13:40

↑ halogan:
Díky :), jinak myslím, že tam má být $\int \frac{f'(x)}{f(x)}\,\mathrm{d}x = \ln |f(x)| + C$

halogan · 25. 06. 2011 13:44

↑ Alivendes:

Na VŠ (a na některých středních školách, zdravím do Plzně a do Brna) se většinou používá přirozený logaritmus, který se značí 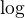$\log$ , dekadický pomálu. I já mám na mysli ten přirozený.

lucik.kicul · 25. 06. 2011 13:44

↑ halogan:
mohla bych ještě poprosit, jestli by jste mi mohli napsat postup u příkladu 2? Stále mi to nevychází a nevím, kde mám chybu

Alivendes · 25. 06. 2011 13:47

↑ halogan:
Tak to nevím, nejsem na vysoké škole :)..

halogan · 25. 06. 2011 13:47

↑ lucik.kicul:

Jednička je tedy v pohodě?

U dvojky se na to jde obdobně. Vytkneme trojku z čitatele (a před integrál) a můžeme použít stejný trik.

$\frac{3x -1}{x+2} = 3 \cdot \frac {x - \frac 13}{x+2} = 3 \cdot \frac {x + 2 - 2 - \frac 13}{x+2} = \cdots$

lucik.kicul · 25. 06. 2011 13:52

↑ halogan:
s tím prvním příkladem nic moc =(, a u druhého příkladu mi stále nedochází jak na ten parciální zlomek =(

Alivendes · 25. 06. 2011 13:54

↑ lucik.kicul:
Tak se podívej na postup, který jsem popsal já, upřímně také nevidím, co ztoho kolega↑ halogan: nakonec vykouzlí :o)

halogan · 25. 06. 2011 13:54

↑ lucik.kicul:

Tak druhý odložíme, ať se nám to tu neplete. Ten první tedy, kde jste se zasekla?

$\int \frac{x}{x+5}\,\mathrm{d}x = \int \frac{x + 5 - 5}{x+5}\,\mathrm{d}x = \int 1 - \frac{5}{x+5}\,\mathrm{d}x = \int 1\,\mathrm{d}x - \int \frac{5}{x+5}\,\mathrm{d}x$

Sem jste se dostala?

Alivendes · 25. 06. 2011 13:56

↑ halogan:
:) takhle jsi to myslel, jak tam ale použiješ tohle ?
$\int \frac{f'(x)}{f(x)}\,\mathrm{d}x = \ln |f(x)| + C$

halogan · 25. 06. 2011 13:58

↑ Alivendes:

$\int \frac{5}{x+5}\,\mathrm{d}x = 5 \int \frac{1}{x+5}\,\mathrm{d}x$

a $(x+5)' = 1$

takže ten integrál je roven

$5 \log|x+5| + C$ .

Alivendes · 25. 06. 2011 14:01

↑ halogan:
Tak to už by potom asi kolegyně↑ lucik.kicul: poznala, ale nenapadla mě taková úprava :), dávám +

lucik.kicul · 25. 06. 2011 14:02

vidím, že jsem měla chybu hned na začátku, do čitatele jsem nenapsala právě +5 a -5, při výpočtu to tedy nevadí,když si to tam dopíši?, ale když mám v čitateli x+5-5, tak jak dostanu integrál z 1? Můžu poprosit o vysvětlení? Nedošlo se k tomu substitucí za x+5? kdy mi vyjde substituce dx=dt a poté int t-5/t * dt?

halogan · 25. 06. 2011 14:04

↑ lucik.kicul:

Přičtení a odečtení ničemu nevadí, to je ve finále nula, takže to je OK.

Co se týče té jedničky, tak to je klasická úprava výrazu.

$\frac{\mathrm{jabko} + \mathrm{hruska}}{\mathrm{jabko}} = 1 + \frac{\mathrm{hruska}}{\mathrm{jabko}}$

lucik.kicul · 25. 06. 2011 14:08

↑ halogan:
Děkuju za pomoc, snad už mi to bude vycházet

lucik.kicul · 25. 06. 2011 14:31

↑ halogan:
tak počítám ten druhý příklad, výsledek mi vychází: 3x-ln|x+2|+C a má to vyjít 3x-7ln|x+2|+C netuším,kde se vzala ta 7?

halogan · 25. 06. 2011 14:34

Vy tam máte

$3 \frac {x + 2 - 2 - \frac 13}{x+2} = 3 $1 - \frac{\frac 73}{x+2}$ = 3 - \frac{7}{x+2}$

Jasné?

Pokud ne, téma znova označím jako nevyřešené a můžeme to dodělat.

lucik.kicul · 25. 06. 2011 14:36

↑ halogan:
když už teď vím, kde se vzala ta 7, tak jak se přišlo v předešlých krocích k 1/3?

halogan · 25. 06. 2011 14:43

↑ lucik.kicul:

1/3 byla už v zadání. Resp. byla tam jednička, ze které se po vytknutí stala 1/3.

Alivendes · 25. 06. 2011 14:48

↑ lucik.kicul:
Pokud to vtom nevidíš, můžeš použít perpartes jako já na začátku ...

lucik.kicul · 25. 06. 2011 14:49

↑ halogan:
už je mi to jasné, děkuji =)

Matematické Fórum

#1 25. 06. 2011 13:19

Integrace racionálních funkcí

#2 25. 06. 2011 13:30

Re: Integrace racionálních funkcí

#3 25. 06. 2011 13:30 — Editoval Alivendes (25. 06. 2011 13:34)

Re: Integrace racionálních funkcí

#4 25. 06. 2011 13:37 — Editoval halogan (25. 06. 2011 13:39)

Re: Integrace racionálních funkcí

#5 25. 06. 2011 13:40

Re: Integrace racionálních funkcí

#6 25. 06. 2011 13:44

Re: Integrace racionálních funkcí

#7 25. 06. 2011 13:44

Re: Integrace racionálních funkcí

#8 25. 06. 2011 13:47

Re: Integrace racionálních funkcí

#9 25. 06. 2011 13:47

Re: Integrace racionálních funkcí

#10 25. 06. 2011 13:52

Re: Integrace racionálních funkcí

#11 25. 06. 2011 13:54

Re: Integrace racionálních funkcí

#12 25. 06. 2011 13:54

Re: Integrace racionálních funkcí

#13 25. 06. 2011 13:56

Re: Integrace racionálních funkcí

#14 25. 06. 2011 13:58

Re: Integrace racionálních funkcí

#15 25. 06. 2011 14:01

Re: Integrace racionálních funkcí

#16 25. 06. 2011 14:02

Re: Integrace racionálních funkcí

#17 25. 06. 2011 14:04

Re: Integrace racionálních funkcí

#18 25. 06. 2011 14:08

Re: Integrace racionálních funkcí

#19 25. 06. 2011 14:31

Re: Integrace racionálních funkcí

#20 25. 06. 2011 14:34

Re: Integrace racionálních funkcí

#21 25. 06. 2011 14:36

Re: Integrace racionálních funkcí

#22 25. 06. 2011 14:43

Re: Integrace racionálních funkcí

#23 25. 06. 2011 14:48

Re: Integrace racionálních funkcí

#24 25. 06. 2011 14:49

Re: Integrace racionálních funkcí

Zápatí