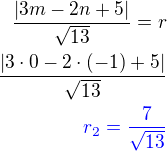Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 27. 06. 2011 11:00 — Editoval Sulfan (27. 06. 2011 11:00)
Re: Rovnice kružnice
↑ Miki314: Co to zkusit takto: Ty dvě zadané přímky jsou různoběžné a protínají se v jednom bodě. Tento bod (X) lehko zjistíme, a také zjistíme směrové vektory obou přímek (u,v). Z těchto vektorů vyrobíme jednotkové a vektorově je sečteme. Výsledný vektor bude vektor w. Tím získáme parametrické vyjádření přímky (bod X a vektor w), která je osou úhlu, který obě přímky svírají (tady pozor, ty přímky budou ve skutečnosti dvě, pro každý úhel jedna - pro menší a pro větší, vektory tedy budeme sčítat dvakrát, podruhé s jeho násobkem -1). Tuto přímku jen protneme s přímkou, na které leží střed a máme souřadnice středu.
Edit: psal jsem to dlouho ... :)
Offline
#5 27. 06. 2011 12:07
Re: Rovnice kružnice
↑ Sulfan: A pro tu osu "druhého" úhlu, jak jsem zmiňoval v #2, je třeba w konstruovat z u a -v, tedy stejně dlouhé (třeba normované, proč ne) vektory u a v odečíst.
Lze samozřejmě řešit i v případě, kdy se má kružnice dotýkat dvou rovnoběžek, tedy průsečík těch zadaných přímek být nemusí (resp. je v nekonečnu).
Offline
#6 27. 06. 2011 12:22 — Editoval Honzc (27. 06. 2011 13:01)
Re: Rovnice kružnice
Offline

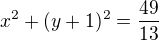 a
a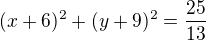
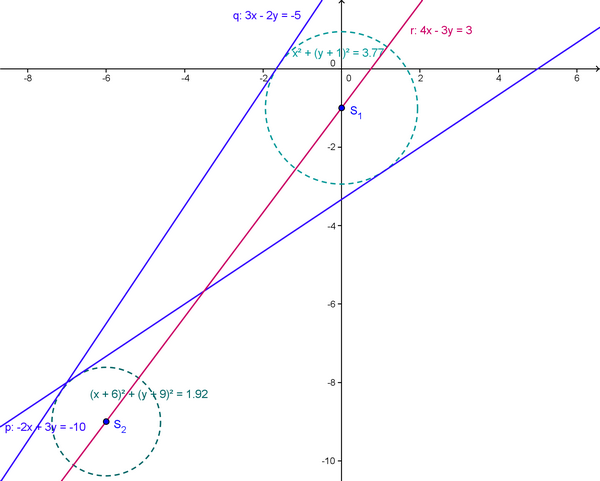
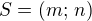 leží na přímce
leží na přímce  tedy platí:
tedy platí: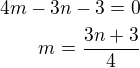
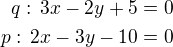 stejnou vzdálenost tedy musí platit:
stejnou vzdálenost tedy musí platit: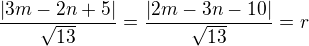 tj.
tj.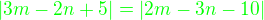 - dosadíme rovnici 1) a po úpravách dostaneme:
- dosadíme rovnici 1) a po úpravách dostaneme: