Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 20. 06. 2011 14:24 — Editoval BakyX (20. 06. 2011 14:55)

BakyX
Cat Lover & S.O.A.D. Lover
Příspěvky: 3416
Škola: UPJŠ
Pozice: Študent
Reputace:   158 
 

Suma s členmi aritmetickej postupnosti

Nech 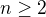$n \ge 2$ je dané prirodzené číslo, $a_0,a_1, ..., a_n$ sú po sebe nasledujúce členy aritmetickej postupnosti. Vypočítajte hodnotu súčtu

$S=\sum^n_{k=0} (-1)^k.{n \choose k}a_k$

Túto úlohu som ešte nevyriešil, ale práve idem na to :)

EDIT: Dúfam, že takýmito to úlohami neotravujem veľmi..

Autor skryl část textu. Zobrazit/skrýt!

1^6 - 2^6 + 3^6 = 666

Offline

  • (téma jako vyřešené označil(a) BakyX)

#2 28. 06. 2011 08:36

musixx
Místo: Brno
Příspěvky: 1771
Reputace:   45 
 

Re: Suma s členmi aritmetickej postupnosti

Při standardním značení jde o součet 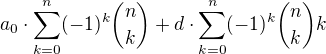$a_0\cdot\sum_{k=0}^n(-1)^k{n\choose k}+d\cdot\sum_{k=0}^n(-1)^k{n\choose k}k$. Stačí uvážit určité vhodné binomické rozvoje, resp. symetrii kombinačních čísel. wolframalpha může napovědět.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson