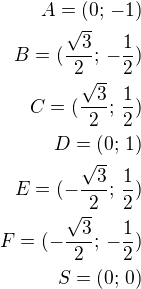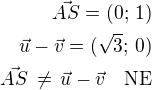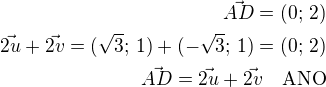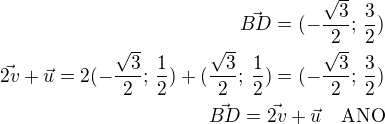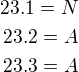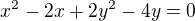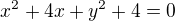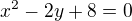Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 06. 2011 14:58
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Řešení státní maturity 2011 vyšší obtížnost
Zadání: Součet dvou čísel je 100. Dělíme-li první číslo sedmi, dostaneme stejný výsledek, jako když druhé číslo vydělíme osmnácti.
Řešení: Označíme první číslo x, druhé y. Pak zřejmě platí: 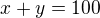
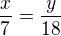
Řešíme tedy soustavu rovnic: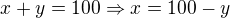
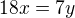
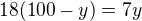
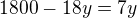
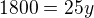
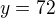
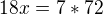
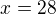
Offline
#5 30. 06. 2011 15:02 — Editoval Hanis (30. 06. 2011 15:14)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Řešení státní maturity 2011 vyšší obtížnost
Zadání: Určete reálné číslo r v zápisu rovnoběžných přímek p a q, jestliže platí: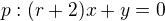
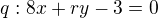
Uveďte všechna řešení.
Řešení:
Dvě přímky jsou rovnoběžné právě tehdy, když jejich normálové vektory jsou lineárně závislé.
normálový vektor přímky 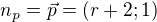
normálový vektor přímky 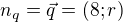
Tyto vektory musí být lineárně závislé, tedy 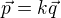
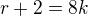
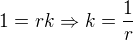
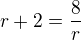
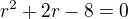
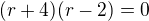
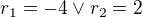
Offline
#6 30. 06. 2011 15:04 — Editoval Hanis (30. 06. 2011 15:16)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Řešení státní maturity 2011 vyšší obtížnost
Zadání:V intervalu  najděte všechan řešení rovnice:
najděte všechan řešení rovnice: 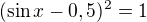
Řešení:Substituce 
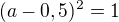
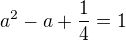
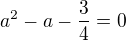
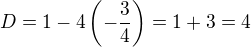
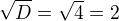
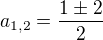
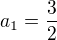
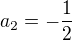
Resubstituce: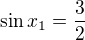
Obor hodnot fce sinus je  , tedy rovnice
, tedy rovnice 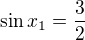 nemá řešení.
nemá řešení.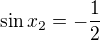
Víme, že fce sinx nabývá záporných hodnot v III. a IV, kvadrantu, dále víme, že 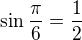 .
.
Tedy 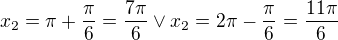
Offline
#7 30. 06. 2011 17:42 — Editoval Hanis (30. 06. 2011 17:59)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Řešení státní maturity 2011 vyšší obtížnost
Zadání: Ve firmě jsou zaměstnanci rozděleni do tří skupin. V první skupině, v níž je 12% zaměstnanců, je průměrný měsíční plat 40000Kč, ve druhé skupině 35000Kč a ve třetí skupině 25000Kč. Průměrný měsíční plat všech zaměstnanců firmy je 33000Kč.
Kolik % zaměstnanců je ve třetí skupině?
Řešení:Označme:
x - jaká část zaměstnanců je ve druhé skupině
y - jaká část zaměstnanců je ve třetí skupině
V první skupině je 12%=0,12. Je zřejmé, že musí platit 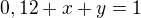
Dále použijeme vtah pro vážený průměr: 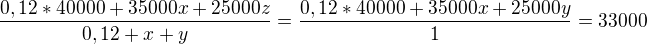
Řešíme tedy soustavu rovnic: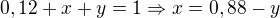
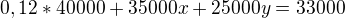
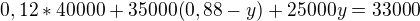
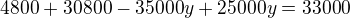
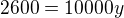
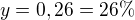
Offline
#8 30. 06. 2011 18:02 — Editoval Hanis (24. 04. 2012 23:09)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Řešení státní maturity 2011 vyšší obtížnost
Zadání:Nekonečná posloupnost 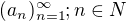 je určena prvním členem
je určena prvním členem 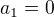 a rekurentním vztahem:
a rekurentním vztahem: 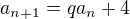
Řešení:
1.) Vyjádřete další tři členy 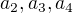 v závislosti na veličinách
v závislosti na veličinách 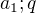 a výrazy upravte tak, aby neobsahovaly závorky.
a výrazy upravte tak, aby neobsahovaly závorky.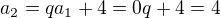
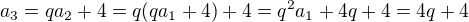
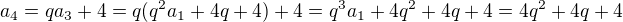
2.)Určete všechny reálné hodnoty q, pro níž je posloupnost 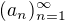 konvergentní.
konvergentní.
Odvodíme si vzorec pro n-tý člen.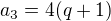
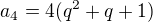
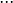
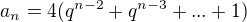
V závorce je částečný součet členů geometrické posloupnosti. Tato geometrická řada je konvergentní, pokud |q|<1
3.) Pro 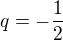 vypočtěte
vypočtěte 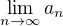 .
.
Pro q=-1/2 dostáváme: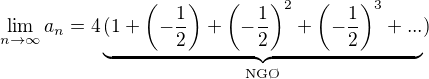
Tato NGŘ je konvergentní, protože |q|=0,5<1, proto existuje součet: 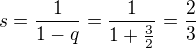
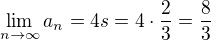
Offline
#11 01. 07. 2011 11:48 — Editoval Annnnnd (01. 07. 2011 11:51)
Re: Řešení státní maturity 2011 vyšší obtížnost
to na tn.cz byla ta cvicna verze co vydal cermat. toto co se resi v tematu to je ta co byla ted u maturit nebo jinak receno "ostra verze" kterou meli matutanti. a pak je ta s PUP "Matematika vyssi pro zaky s priznanym uzpusobenim podminek". a priklady odpovidaji narocnosti te normalni vyssi verzi (ta co je v tomto tematu vyresena) a i bych rekl ze nektere priklady sou tezsi, takze nechapu proc to takhle komplikuji, nicmene vcera jsem ji resil tak mohu sem hodit reseni nejake.
Offline
#12 02. 07. 2011 18:34 — Editoval Annnnnd (02. 07. 2011 18:40)
Re: Řešení státní maturity 2011 vyšší obtížnost
MATEMATIKA 2011 VYŠŠÍ ÚROVEŇ OBTÍŽNOSTI (PRO ŽÁKY S PŘIZNANÝM UZPŮSOBENÍM PODMÍNEK); KÓD TESTU: MAMVD11C0T03
Úloha 1;2
Zadání:
Řešení:
Offline
#13 02. 07. 2011 18:40
Re: Řešení státní maturity 2011 vyšší obtížnost
Offline
#14 02. 07. 2011 18:42
Re: Řešení státní maturity 2011 vyšší obtížnost
Offline
#15 02. 07. 2011 19:19 — Editoval Annnnnd (02. 07. 2011 19:58)
Re: Řešení státní maturity 2011 vyšší obtížnost
Úloha 5;6
Zadání č.5:
Zadání č.6
Řešení 5;6:
Offline
#16 02. 07. 2011 19:33
Re: Řešení státní maturity 2011 vyšší obtížnost
Offline
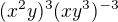
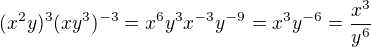
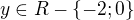 maximálně zjednodušte:
maximálně zjednodušte: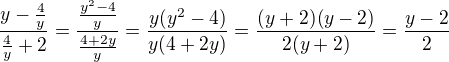
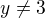 platí předpis
platí předpis 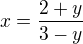 . Z předpisu vyjádřete proměnnou y pro
. Z předpisu vyjádřete proměnnou y pro 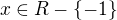 .
.
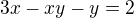

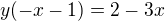
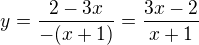









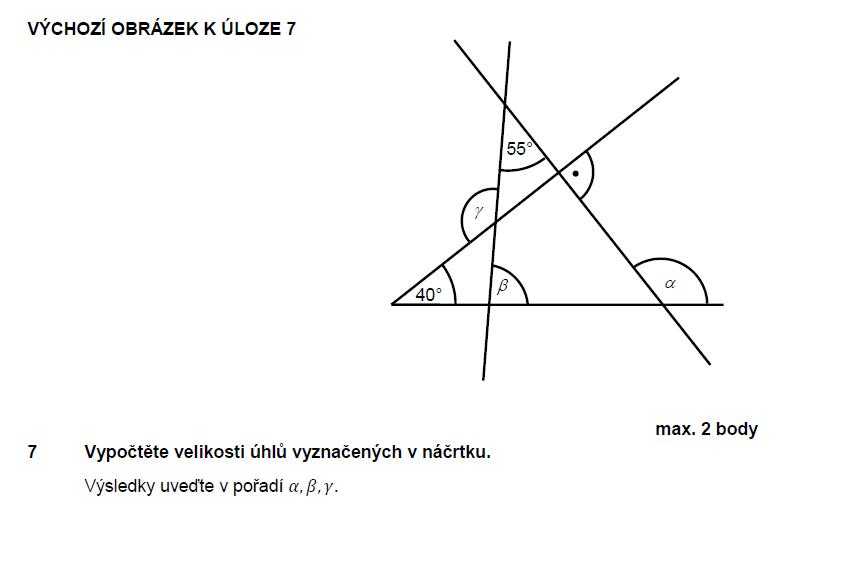


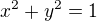 potom vrcholy budou mít dle obrázku souřadnice:
potom vrcholy budou mít dle obrázku souřadnice: