Matematické Fórum

richard44

Úvodní příspěvek k úloze je zde.

4. Narýsuj graf funkce $y=-\frac13|x|+\frac52$ a zapiš obor hodnot.

jelena · 26. 06. 2011 09:03

↑ richard44:

Zdravím,

v úvodním příspěvku je EDIT váženého Administrátora, ovšem toto zadání není běžné pro ZŠ, proto jen upřesnění - skutečně je v zadání zápis pro dolní celou část nebo pro absolutní hodnotu, a to tak: $y=-\frac13|x|+\frac52$

Děkuji.

Alivendes · 26. 06. 2011 09:17

↑ jelena:
Když už jsme u toho, jak se takový graf sestrojuje ? Jak by třeba vypadala derivace nebo integrál?

richard44

kecičky netýkající se příkladu Zobrazit/skrýt!

richard44

↑ Alivendes:
Tak to fakt nevím. Upřímně řečeno, o pojmu derivace jsem zatím slyšel jenom ve filmech - tak jako všichni mí vrstevníci.

kecičky netýkající se příkladu Zobrazit/skrýt!

jelena · 26. 06. 2011 10:02

↑ Alivendes: přejdi na anglický text članku Wikipedie a studuj :-) Případně si založ vlastní téma (může být i v sekci Zajímavé úlohy ze SŠ).

↑ richard44: děkuji za rozptylující komentáře :-) Osmileté gymnázium je snová představa, která (zejména díky kolegovi Hanisovi se momentálně podařilo dosáhnou, v pondělí půjdeme i na 1. rodičovskou schůzku), ovšem vidím to jako těžký boj minimálně pro první období, než se pochopí jiný přístup ke studiu (samostatná soustavná příprava).

Pokud jsi kvarta osmiletého gymnázia, potom úlohy můžeš dávat do sekce SŠ, bude to více přiměřené.

Se samotnou funkci ↑ s absolutní hodnou: - věřím, že pomůže někdo z kolegů, děkuji.

Alivendes

↑ jelena:
Dobrý nápad, náhodou nevíš, jak se řekne dolní celá část anglicky :) ?

kolega ↑ Hanis: je synek :) ? přeji hodně štěstí, smím se zeptat, které osmileté gymnasium?

Hanis · 26. 06. 2011 11:05 — Editoval Hanis (26. 06. 2011 11:07)

↑ richard44:
K problému:
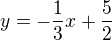Funkce, v níž se vyskytuje $|x|$ jsou sudé. Tzn. že jsou osově souměrné podle osy y. Čili narýsuješ graf fce $y=-\frac13x+\frac52$ v kladné části osy x, následně doplníš graf v záporné části pomocí osové souměrnosti.

EDIT: ↑ Alivendes: Wiki

jelena · 26. 06. 2011 11:11

↑ Alivendes:

zcela OT Zobrazit/skrýt!

Náhled na příspěvek kolegy Hanise - hodného a ochotného vyučujícího (zdravím) vidím, ale už to tady nechám.

Hanis · 26. 06. 2011 11:13

↑ jelena:
Angličtina si taky hlavu neláme a stanovila si podlahu a strop :-)

Alivendes · 26. 06. 2011 11:15

↑ Hanis:
:) také jsem si již všiml

((:-)) · 02. 07. 2011 08:20 — Editoval ((:-)) (02. 07. 2011 09:13)

Graf tejto funkcie sa robí tak, ako píše Hanis, ale je možný aj iný postup:

Podrobný postup: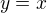

$y = x$ priamka, ktorá pretína os y v bode 0 a os x tiež v bode 0, leží na nej napríklad bod [3; 3] (x zvolíš, y rátaš z rovnice)

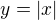$y = |x|$ v predchádzajúcom grafe sa časť, ktorá je pod osou x "preklopí" nad ňu

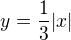$y = \frac{1}{3} |x|$ každý bod grafu zmení svoju hodnotu y na tretinu, vetvy grafu "klesnú" bližšie k osi x

$y = - \frac{1}{3} |x|$ všetky hodnoty y zmenia znamienka na opačné, graf sa teda celý "preklopí" pod os x

$y = - \frac{1}{3}|x| + \frac52$ všetky hodnoty y bodov grafu sa posunú o $\frac{5}{2}$ (nahor)

Graf z WA: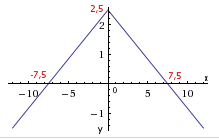

priesečník s osou x sa vyráta tak, že sa v rovnici funkcie položí y = 0 (takúto súradnicu y majú všetky body osi x)

Obor hodnôt sú všetky hodnoty y, ktoré sa môžu vypočítať z rovnice funkcie pre všetky dovolené hodnoty x

- podľa grafu vypočítané hodnoty y siahajú od mínus nekonečna po 2,5, platí teda $H(f) = (-\infty; 2,5 >$