Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti s odmocninami (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 07. 2011 12:19
Limita posloupnosti s odmocninami
Ahoj,
chtěl bych poprosit o nápovědu, jak pokračovat v jedné, pro mě zapeklitější, limitě, která vypadá následovně:
Začal jsem tak, že jsem výraz roznásobil  a zároveň z prvních dvou členů vytkl
a zároveň z prvních dvou členů vytkl  :
:![kopírovat do textarea $\lim_{n->\infty}\left [ n\cdot (\sqrt{1+\frac{1}{n}}+2)-3\sqrt{n^2+2n} \right ]$](/mathtex/09/09d0f3c75f165f368b85ebb797185a48.gif)
Potom jsem celý výraz v limitě rozšířil výrazem 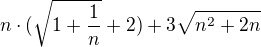 , abych v čitateli dostal oblíbený vzorec
, abych v čitateli dostal oblíbený vzorec  :
:
Limitu jsem upravil dále na tvar:![kopírovat do textarea $\lim_{n->\infty} \frac{n\left [ \left n\cdot (\sqrt{1+\frac{1}{n}}+2 \right )^2 -9n-18 \right ]}{n\left ( \sqrt{1+\frac{1}{n}}+2+3\sqrt{1+\frac{2}{n}} \right )}$](/mathtex/e8/e8e0d8b2e73a086d64a935e9acf1415f.gif)
A po několika dalších řádcích úprav mi vyšlo (vím, že je to až sem dobře):
Ale moc jsem si nepomohl, spíše jsem se dostal z bláta do louže, protože mi v čitateli vznikl opět neurčitý výraz  .
.
Nemáte nápad, jak pokračovat?
Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti s odmocninami (TOTO TÉMA JE VYŘEŠENÉ)


