Matematické Fórum

rimer · 03. 07. 2011 16:12

Zdravim, mam najst pravouholnik ktory, ktory ma pri danom obvode maximalny obsah
mam teda najst maximum funkcie $S(o)=\frac{or}{2}$ kde r je polomer vpisanej kruznice?
dakujem

BakyX · 03. 07. 2011 16:23 — Editoval BakyX (03. 07. 2011 16:23)

Je lepšie si vyjadriť obsah pomocou obvodu a nejakej strany - najlepšie prepony. Pre polomer vpísanej kružnice v pravouhlom trojuholníku platí:

$r=\frac{a+b-c}{2}=\frac{o-2c}{2}$

jelena · 03. 07. 2011 16:27

↑ BakyX:

pravouholník je obdlžnik (ale je to tajné :-) Zdravím.

BakyX · 03. 07. 2011 16:30

↑ jelena:

jA SOM MYslel, že pravouhlý trojuholník..:D

rimer · 03. 07. 2011 16:36

aha a ja som si to pomylil s pravidelnym n-uholnikom :D

miso16211 · 03. 07. 2011 17:04

hmmm, to akoze bude x= obvod y=obsah a chceš najsť predpis. Ale tak toto neviem.

Phate · 03. 07. 2011 17:12 — Editoval Phate (03. 07. 2011 17:14)

↑ miso16211:
Proc sem teda pises, kdyz to nevis?
Pravouhelnik = obdelnik, jak zminila jelena, znas jeho obvod, ten je mimo jine 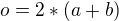$o=2*(a+b)$ , odtud si vyjadris $a$ a dosadis do obsahu 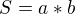$S=a*b$ a derivujes podle b a hledas maximum. Mimochodem zustane ti tam ve vyjadreni o, s tim pracujes jako konstantou

rimer · 03. 07. 2011 17:19

jasne kedze pravouholnik je obdlznik uz to viem, myslel som povodne ze je to n-uholnik, vdaka

Matematické Fórum

#1 03. 07. 2011 16:12

maximalny obsah

#2 03. 07. 2011 16:23 — Editoval BakyX (03. 07. 2011 16:23)

Re: maximalny obsah

#3 03. 07. 2011 16:27

Re: maximalny obsah

#4 03. 07. 2011 16:30

Re: maximalny obsah

#5 03. 07. 2011 16:36

Re: maximalny obsah

#6 03. 07. 2011 17:04

Re: maximalny obsah

#7 03. 07. 2011 17:12 — Editoval Phate (03. 07. 2011 17:14)

Re: maximalny obsah

#8 03. 07. 2011 17:19

Re: maximalny obsah

Zápatí