Matematické Fórum

elopin · 08. 07. 2011 20:22

Prosim o strucnou odpoved, asi je to matematicka banalita, ale nikde nemuzu najit logicke vysvetleni tohoto pravidla.

resim y=f(x+a)
y=f(x) + a

chapu a vidim, ze po ose y to jde a > 0 = posun nahoru a a < 0 = posun dolu, ale nemuzu pochopit, proc na ose x je to obracene a > 0 = posun doleva a a < 0 = posun doprava

budu rad i za nejaky odkaz

Olin · 08. 07. 2011 20:32 — Editoval Olin (08. 07. 2011 20:32)

Když budu mít třeba $a = 1$ a chci vědět, pro jaké $x$ bude mít argument funkce hodnotu 3, tak u $f(x)$ to bude pro $x = 3$ a u $f(x+a)$ pro $x = 2$ , takže to "nastane dřív" (pro menší hodnotu $x$ ), proto posun doleva.

No nevím, jestli takové vysvětlení může někomu pomoct :-)

Annnnnd · 08. 07. 2011 20:34

jestli mohu doporucit namaluj si napr. fci y = 2^(x-3) tabulkovou metodou a uvidis. udelej si Df -6;6

pepa999

Představ si, že máš funkci 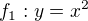$f_1:y=x^2$ . A představ si její graf. Můžeš si ho klidně aji nakreslit. Teď si vem druhou funkci, tady tuto: $f_2:y=(x-1)^2$ . A teď si představ, jak budeš sestrojovat její graf. Můžeš si ho zase klidně aji zkusit sestrojit. Důvod, proč se ten graf posouvá "opačně, než by měl" je následující. 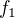Ty si ten graf totiž můžeš sestrojit tak, že si nejdřív narýsuješ graf té první funkce $f_1$ a následně začneš rýsovat graf funkce 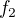$f_2$ tímto způsobem:
1. Vybereš si libovolné číslo $x$ , pro které chceš sestrojit bod grafu(na ose X)
2. Teď se posuneš o 1 směrem DO LEVA, takže se dostaneš k číslu 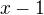$x-1$ na ose X
3. Na kolmici k ose X z bodu, na kterém se nacházíš (obraz čísla 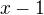$x-1$ na ose X)
leží bod grafu funkce 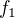$f_1$ , jehož y-ová souřadnice je 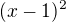$(x-1)^2$ , což je hodnota,
kterou chceme přiřadit našemu $x$ .
4. Posuneme tento bod o 1 směrem DO PRAVA a tento bod se bude nyní nacházet na kolmici k
ose X, která prochází obrazem čísla $x$
5. Tento bod je bodem grafu funkce 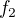$f_2$ , protože jeho x-ová souřadnice je $x$ a y-ová souřadnice
je 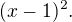$(x-1)^2.$

Tento postup platí pro každý bod, a proto graf funkce 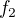$f_2$ je posunutím grafu funkce 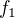$f_1$ o 1 směrem DO PRAVA.

Pokud bys to chtěl vysvětlit ještě trochu jinak, trochu jednodušeji bez nějaké teorie, tak si představ opět graf funkce 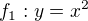$f_1:y=x^2$ a potom ještě graf funkce $f_2:y=(x-15)^2$ , že jsou oba narýsovány v jedné soustavě souřadnic...graf první funkce si předpokládám umíš dobře představit, je to parabola, která má vrchol v bodě [0,0] a směřuje nahoru.....co ale ta druhá funkce? Ta musí být posunuta o 15 směrem do prava a ne do leva, protože teprve pro x = 15 nabývá té hodnoty co ta první pro x = 0....teprve pro x = 16 nabývá té hodnoty co ta první pro x = 1.......atd........takže je to ta stejná parabola, akorát má vrchol v bodě [15,0]...

check_drummer · 08. 07. 2011 23:17

{[x,f(x+a)]}={[t-a,f(t)]} (t:=x+a) a body množiny vpravo jsou o -a posunuté po ose x oproti {[x,f(x)]}, což je graf f(x).

check_drummer · 08. 07. 2011 23:26

Může být zajímavé zkoumat graf složené funkce f(g(x)), g(x)=x+a je potom speciální případ.

elopin · 09. 07. 2011 06:46

Dekuji vam vsem, uz to chapu a prijde mi to logicke, od kazdeho jsem si vzal neco a check_drummer to pekne shrnul do zapisu.

miso16211 · 09. 07. 2011 15:29

keď chceš mužeš me zkontaktovať, tiež sa zaoberám tou problematikou

musixx · 10. 07. 2011 08:48 — Editoval musixx (10. 07. 2011 08:59)

↑ elopin: Taky přispěju, a to na původní dotaz, kdy je "záhada", že "na ose x je to obráceně". Není, osa x není v tomto smyslu nijak odlišná od osy y. Určitě aspoň někteří, co sem přispěli, to ví, ale jen jaksi -- zdá se mi -- léčili následky a ne příčinu.

Tak tedy: Není vhodné se na situaci dívat jako na

y=f(x+a)

a

y=f(x) + a

a to protože v prvním případě se to 'a' přičítá k x, zatímco ve druhém tomu tak u y není. Druhý případ je třeba vidět jako

y-a=f(x)

a pak se jak ve směru osy x, tak ve směru osy y posouvá vždy stejně.

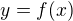Obecně: Graf funkce $y-y_0=f(x-x_0)$ je od grafu funkce $y=f(x)$ posunut o $x_0$ ve směru osy x a o $y_0$ ve směru osy y.

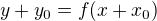EDIT: Poznámka pro méně zkušené: Obecná forma $y-y_0=f(x-x_0)$ , kterou jsem použil, se takto běžně v literatuře používá (v různých kontextech) i s těmi mínusy. Ukazuje se totiž, že je to přirozenější, než kdyby tam byly plusy. Souvisí to s pojmem kladné matematické orientace, ale to už tady rozepisovat nebudu. I v tom, co jsem už napsal, je vidět, že kdybych se bavil o funkci $y+y_0=f(x+x_0)$ , pak by posuny o $x_0$ a $y_0$ nebyly ve směrech orientací os x a y, ale opačně.