Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » A combinatorial identity (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 07. 2011 18:28
A combinatorial identity
Prove that for every non-negative integer  the following identity holds true:
the following identity holds true:
__________
Please, use only elementary techniques not based on induction!
Offline
- (téma jako vyřešené označil(a) Marian)
#2 08. 07. 2011 20:43
#3 08. 07. 2011 21:36
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: A combinatorial identity
"Máte úhel beta." "No to nemám."
Offline
#4 11. 07. 2011 13:26
Re: A combinatorial identity
↑ stuart clark:↑ check_drummer:
Nice! My approach was identical with that of stuart clark, i.e., the consideration of coefficients of a binomial expansion.
Note that the given identity can be written in a more interesting form as
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » A combinatorial identity (TOTO TÉMA JE VYŘEŠENÉ)

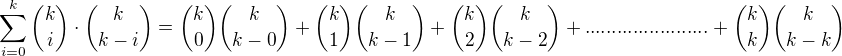
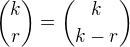
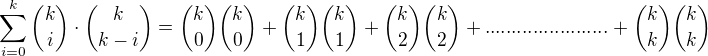

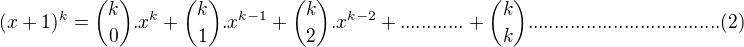
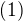 and
and 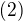 and equating coefficient of
and equating coefficient of 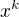
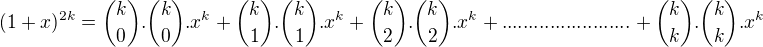
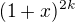 is
is 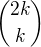
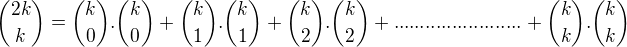
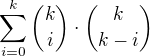 .
.