Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » real solution (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 07. 2011 16:40
- stuart clark

- Příspěvky: 1015
- Reputace: 7
real solution
number of real solution of the equation 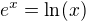
Offline
- (téma jako vyřešené označil(a) byk7)
#3 14. 07. 2011 17:55 — Editoval halogan (14. 07. 2011 18:45)
#4 15. 07. 2011 04:07
#5 15. 07. 2011 08:27
#6 15. 07. 2011 09:24
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: real solution
A bit simpler solution might be to leverage the symmetric quality of inverse functions.
If we know that these two functions are both continuous and symmetric about the line 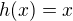 , if we cannot find an intersection of
, if we cannot find an intersection of  and, say,
and, say,  , we get our answer. This will be a bit simpler, we will use the same theorem as above (
, we get our answer. This will be a bit simpler, we will use the same theorem as above ( and
and  are parallel as well).
are parallel as well).
So either we use this geometric quality of inverse functions that may need a proof itself, or we use twice the same theorem we used in this proof anyway.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » real solution (TOTO TÉMA JE VYŘEŠENÉ)

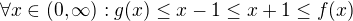 ,
,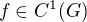 . Then
. Then  is strictly concave if and only if
is strictly concave if and only if
 .
.