Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 07. 2011 22:44
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Variační počet v mechanice
Zdravím uživatele fóra, kteří jsou aktivní i během okurkové sezony. :) Četl jsem si něco o základech variačního počtu a narazil na zajímavou úlohu:
Obr. (omlouvám se za kvalitu)
Není mi jasné, jak se k tomu funkcionálu dospělo. Nejspíš půjde o vyjádření deformační energie nosníku, kterou se snažíme minimalizovat, ale konkrétně bych to dohromady nedal. Taky není uveden význam konstant
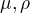 ani způsob zatížení nosníku. Dešifrovat tenhle „motivační“ příklad možná nemá cenu, snad jen kdyby někdo na první pohled věděl. Spíš bych se chtěl zeptat na nějaké (nejlépe internetové) zdroje, kde by podobné úlohy byly vyloženy i s teorií (ČJ, AJ, NJ). Předem díky!
ani způsob zatížení nosníku. Dešifrovat tenhle „motivační“ příklad možná nemá cenu, snad jen kdyby někdo na první pohled věděl. Spíš bych se chtěl zeptat na nějaké (nejlépe internetové) zdroje, kde by podobné úlohy byly vyloženy i s teorií (ČJ, AJ, NJ). Předem díky! Offline
- (téma jako vyřešené označil(a) FliegenderZirkus)
#2 16. 07. 2011 23:39 — Editoval Pavel Brožek (17. 07. 2011 00:02)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Variační počet v mechanice
↑ FliegenderZirkus:
Téměř jistě bude 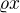 odpovídat potenciální energii (
odpovídat potenciální energii ( bude délková hustota) a
bude délková hustota) a 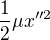 bude odpovídat nějaké energii pružnosti (oboje na jednotku délky samozřejmě).
bude odpovídat nějaké energii pružnosti (oboje na jednotku délky samozřejmě).
Možná je trochu matoucí, že x je tady svislá výchylka a 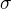 parametrizuje bod na nosníku.
parametrizuje bod na nosníku. 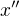 je tak vlastně „míra ohnutí v bodě“ a je to přenásobené nějakou konstantou
je tak vlastně „míra ohnutí v bodě“ a je to přenásobené nějakou konstantou 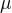 , která udává, jak moc těžké je daný materiál o dané tloušťce atd. ohnout.
, která udává, jak moc těžké je daný materiál o dané tloušťce atd. ohnout.
Něco možná najdeš zde, ale ten text nijak neznám, jen jsem ho teď v rychlosti našel.
Offline
#3 17. 07. 2011 00:08
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Variační počet v mechanice
↑ Pavel Brožek:
To by znamenalo, že zatížení je jen od vlastní tíhy a žádné vnější není? Tak to asi bude. My jsme v pružnosti a pevnosti většinou vlastní tíhu zanedbávali, protože vnější zatížení byla mnohem větší, proto mě to zmátlo.
Obecně mi není jasné, jak se do těchto „energetických“ metod započítá samotná statická rovnováha, neboli jak mi z minimalizace součtu nějakých dvou energií vyjde soustava, která je automaticky v rovnováze. Proto by mě konkrétně zajímalo, jak se k těm integrovaným výrazům došlo. Zkusím taky ten Google, třeba něco vypadne ;)
Offline
#4 17. 07. 2011 00:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Variační počet v mechanice
↑ FliegenderZirkus:
Ano, jsem přesvědčen, že se myslí nosník zatížený pouze vlastní vahou.
Pokud je systém v nějakém (obecně nerovnovážném) stavu v klidu s určitou celkovou potenciální energií, tak může být samovolně malinko vychýlen jen do podobného stavu s nižší potenciální energií (zvýší se tím jeho kinetická energie). Po vychýlení se ale jeho kinetická energie už nemusí nutně přeměnit zpět na potenciální, může se přeměnit na teplo. Postupným tlumením se dostaneme do klidu v minimu potenciální energie, tam pak budeme v rovnováze, protože jakkoliv bychom se z rovnovážné polohy vychýlili, vzrostla by potenciální energie, což ale ze zákona zachování nemůže. A to je to, co počítáme – hledáme minimum celkové potenciální energie. Přitom „proměnná“, kterou měníme, je tvar nosníku.
Ten funkcionál je vlastně závislost celkové potenciální energie na tvaru nosníku. Bez ohledu na to, jestli je nosník v rovnováze, můžeme spočítat jeho celkovou energii pomocí toho vzorce s integrálem. To, že se integruje, snad problém není – celková energie je prostě součet energie všech kousků nosníku. To, že malý kousek nosníku má energii 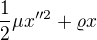 , asi nebude těžké odvodit, intuitivně jsem to snad dostatečně popsal v minulém příspěvku.
, asi nebude těžké odvodit, intuitivně jsem to snad dostatečně popsal v minulém příspěvku.
Nejsem si jistý, jestli ti odpovídám na tvůj dotaz :-). Možná ti říkám jen triviální věci, které už znáš, ale snad si z toho něco vybereš :-).
Offline
#5 17. 07. 2011 11:46
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Variační počet v mechanice
↑ Pavel Brožek:
Na můj dotaz odpovídáš, dokonce bych řekl tak akorát na úrovni, které jsem schopen porozumět.
Ta deformační energie od ohybu by mohla vypadat takhle:
Z diferenciální rovnice průhybové čáry (str.48 výše odkazovaného textu) 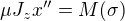 máme
máme 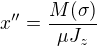 , kde
, kde 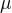 je modul pružnosti v tahu,
je modul pružnosti v tahu,  je kvadratický moment setrvačnosti k ose
je kvadratický moment setrvačnosti k ose  (kolmé na
(kolmé na 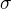 a
a  ) a
) a 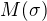 je ohybový moment. Po dosazení
je ohybový moment. Po dosazení 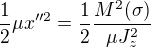 , což je právě deformační enegrie od ohybu v místě o souřadnici
, což je právě deformační enegrie od ohybu v místě o souřadnici 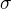 .
.
Připadá mi, že správně by takový výpočet odpovídal situaci: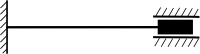 .
.
Kdyby byl totiž nosník na obou koncích vetknutý, tak se deformací prodlouží a vznikne v něm i tahové napětí. Ale je pravda, že tohodle zjednodušení se dopouštíme už tím, že integrujeme od -l do l a ne podél té zakřivené osy.
Co by se změnilo připojením vnější síly F?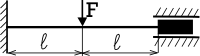
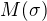 bude pořád neznámá funkce...
bude pořád neznámá funkce...
Klasické řešení takového nosníku by bylo hrozně pracné (je dvakrát staticky neurčitý), proto mně tahle energetická metoda přijde hrozně zajímavá.
Offline
#6 17. 07. 2011 12:19 — Editoval Pavel Brožek (17. 07. 2011 12:46)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Variační počet v mechanice
↑ FliegenderZirkus:
Tipnul bych si, že autoři měli na mysli takový případ, kde prohnutí bude malé, a tam nejspíš půjde zanedbat prodloužení a tahové napětí.
To, že integrujeme od -l do l i když je délka nosníku větší, není zanedbání něčeho – 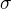 podle mě neznačí vzdálenost od středu nosníku branou po nosníku, ale vodorovnou souřadnici elementu.
podle mě neznačí vzdálenost od středu nosníku branou po nosníku, ale vodorovnou souřadnici elementu.
Připojením vnější síly (můžeme ji realizovat např. zavěšením nějakého závaží o hmotnosti M) vlastně přidáme do celkové energie další člen – potenciální energii.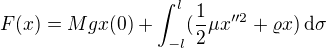
Nevim, jestli z tohohle jde nějak získat nějakou rovnici na způsob Eulerovy rovnice.
Offline
#7 17. 07. 2011 12:46 — Editoval Pavel Brožek (17. 07. 2011 13:15)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Variační počet v mechanice
Šlo by to přepsat takto ( je Diracova delta funkce):
je Diracova delta funkce):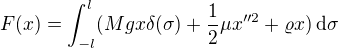
Varírováním a podmínkou nulové variace bychom pak asi dostali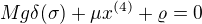 ,
,
po přepsání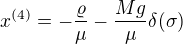 .
.
Z toho bychom jednoduchým integrováním dostali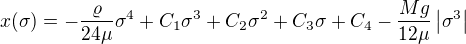 . (Edit: oprava numerické chyby.)
. (Edit: oprava numerické chyby.)
Možná tam ale mám chybu, dělal jsem to dost narychlo.
Offline
#8 17. 07. 2011 13:12
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Variační počet v mechanice
Zkusím to spočítat jiným způsobem a porovnat, ale vypadá to věrohodně.. Asi se k tomu dostanu až zítra, zatím moc děkuju za spolupráci. S tou mojí poznámkou o integrování od -l do l bych se vlastně dostal do problémů spíš u toho upraveného zadání, kde pravý konec nosníku bude mít vodorovnou souřadnici o něco méně než l, ale už během odvozování těch vztahů se použila zjednodušení toho typu, že dílka nosníku se nemění atd., takže to je fakt spíš detail.
Offline
#9 18. 07. 2011 19:09
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Variační počet v mechanice
↑ Pavel Brožek:
Spočítal jsem to metodou deformačních podmínek a vyšlo mi:![kopírovat do textarea $x(\sigma) = \begin{cases}
\frac{1}{24 EJ_z} \left( -\rho l^4-Fl^3+2\rho l^2 \sigma^2+3Fl\sigma^2+2F\sigma^3-\rho \sigma^4 \right) & \ \ \sigma \in [-l,0] \\
\frac{1}{24 EJ_z} \left( -\rho l^4-Fl^3+2\rho l^2 \sigma^2+3Fl\sigma^2-2F\sigma^3-\rho \sigma^4 \right) & \ \ \sigma \in (0,l]
\end{cases}$](/mathtex/1d/1deb3cd104c4e17de48643450cd2f941.gif) ,
,
kde 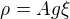 , kde
, kde  je plocha kruhového průřezu,
je plocha kruhového průřezu,  je gravitační zrychlení a
je gravitační zrychlení a  je měrná tíha (
je měrná tíha (![kopírovat do textarea $[ \xi ] =\frac{\mathrm{N}}{\mathrm{m}}$](/mathtex/93/93afce213a673c7f40073721bf2cf29d.gif) ),
),  je modul pružnosti v tahu. Po zavedení absolutní hodnoty a
je modul pružnosti v tahu. Po zavedení absolutní hodnoty a 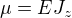 :
: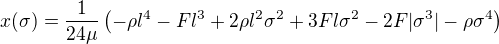 ,
,
což odpovídá jak tvému výsledku, tak při dosazení  výsledku z knihy. Teď zkusím porozumět tomu postupu s funkcí delta, protože ten můj byl (bez nadsázky) na 3 hustě popsané A4 s občasným použitím počítače. :)
výsledku z knihy. Teď zkusím porozumět tomu postupu s funkcí delta, protože ten můj byl (bez nadsázky) na 3 hustě popsané A4 s občasným použitím počítače. :)
Offline
#10 18. 07. 2011 19:23
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Variační počet v mechanice
↑ FliegenderZirkus:
To jsem vážně rád, že to vyšlo stejně :-). Kdybys chtěl nějaký můj krok podrobněji rozepsat, tak není problém.
Offline