Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 07. 2011 20:25
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
jak kreslit grafy funkcí
ahoj, vůbec nemám tucha jak kreslit grafy funkcí, celůé mi to nějak vypadlo...
našla sem si třeba toto: http://ucebnice.krynicky.cz/Matematika/ … funkci.pdf
ale to mi nijak nepomohlo....
a ani z knih sem moc nezmoudřela - jak nakreslit grafy lvadratické, lineární a exponencionální funkce? je na to nějaký obecný postup?
třeba tohle: y
= 2 f (x +1) - 2 = 2 x +1 - 2
co to značí? jak z toho vyluštit graf funkce? a PROČ CPOU ABSOLUTNÍ HODNOTU DO ČÁSTIFUNKCE, KDE ANI MÍNUS NENÍ?
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
- (téma jako vyřešené označil(a) Alenka.Janská)
#2 15. 07. 2011 20:31 — Editoval halogan (15. 07. 2011 20:31)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: jak kreslit grafy funkcí
Moje poznámka se netýká průběhu funkcí, jen té absolutní hodnoty.
Neplatí, že absolutní hodnota jen nějak převrací znaménka, tak to nefunguje. Jde o to, že absolutní hodnota vše záporné převede na kladné. Nic víc, nic míň.
Pokud máš tedy třeba
Tak pro 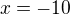 je vnitřek roven -9, takže zde dojde k otočení znaménka, tj.
je vnitřek roven -9, takže zde dojde k otočení znaménka, tj.  .
.
Obecně v tomto případě: pro každé x větší než nebo rovno -1 se nic neděje a absolutní hodnotu můžeme odstranit. Pro x < -1 musíme odstranit absolutní hodnotu tak, že před výraz dáme mínusko, tj.
Offline
#3 15. 07. 2011 21:14 — Editoval ((:-)) (15. 07. 2011 22:45)
Re: jak kreslit grafy funkcí
↑ Alenka.Janská:
Musíš si naštudovať teóriu, tu na podrobné výklady myslím nie je priestor... Na lineárnu funkciu by mala stačiť učebnica ZŠ.
Niektoré funkcie majú grafy "známe": lineárna funkcia má graf priamku, kvadratická má graf parabolu, exponenciálna má tiež typický graf...
Kvadratická funkcia
lineárna funkcia
exponenciálna funkcia
Offline
#4 16. 07. 2011 14:51
- Alenka.Janská
- Příspěvky: 181
- Reputace: 3
Re: jak kreslit grafy funkcí
↑ ((:-)):
díky moc :)
Jo, opravdu si vážím veškeré projevené pomoci... :)
Offline
#5 16. 07. 2011 15:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: jak kreslit grafy funkcí
Také děkuji kolegům.
↑ Alenka.Janská:
Prosím, označuj témata za vyřešená. Děkuji.
Offline
#6 18. 07. 2011 10:36 — Editoval Rumburak (18. 07. 2011 13:58)
Re: jak kreslit grafy funkcí
↑ Alenka.Janská:
K funkcím, jejichž grafy je potřeba umět nakreslit, ještě doplním další:
- logaritmickou funkci  , kde
, kde  ,
,
jejímž grafem je křívka, která je osově souměrná s grafem odpovídající exponenciání funkce  , při čemž osou této souměrnosti je
, při čemž osou této souměrnosti je
přímka o rovnici 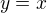 , tj. osa I. a III. kvadrantu,
, tj. osa I. a III. kvadrantu,
- goniometické funkce : sinus, kosinus, tangens, kotangens.
Ale nevím, ve kterém jsi ročníku a co z toho jste už probírali.
Dále (pro pokročilejší):
- K dané funkci 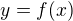 , jejíž graf známe, bychom měli umět nakreslit též grafy funkcí
, jejíž graf známe, bychom měli umět nakreslit též grafy funkcí
 ,
, 
 ,
,  ,
,  ,
, 
( je předepsaná konstanta) na množinách, kde jsou tyto "nové" funkce definovány .
je předepsaná konstanta) na množinách, kde jsou tyto "nové" funkce definovány .
- Známe-li grafy funkcí 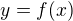 ,
,  , majících společný definiční obor, měli bychom umět nakreslit též graf funkce
, majících společný definiční obor, měli bychom umět nakreslit též graf funkce  .
.
O žádném konkretním studijním materiálu ale nevím, nikdy jsem žádný takový nečetl vyjma partií ve školních učebnicích,
kde jsou zmínené funkce probírány.
PS. Pokud Ti některá formulace v učebnici není jasná, můžeme ji tu probrat.
Ke Tvému dotazu k funkci  :
:
Neuvádíš celé zadání , mohu se domýšlet (ale možná mylně), že úkolem je nakreslit graf funkce f definované rovnicí
 .
.
V tom případě můžeme postupovat tak, že nejprve ji (přičtením dvojky k obšma stranám) zjednodušíme na  .
.
Nyní provedeme substituci  , tj.
, tj.  . Dostaneme novou rovnici
. Dostaneme novou rovnici  , z níž vyjádříme
, z níž vyjádříme  ,
,
což dává předpis pro funkci f va tvaru, na jaký jsme zvyklí:  (proměnnou t jsme změnili na x).
(proměnnou t jsme změnili na x).
Máme tedy sestrojit graf funkce  .
.
Ale opakuji: neznám přesné zadání úlohy a proto je možné, že se mělo řešit něco úplně jiného.
Offline
#7 18. 07. 2011 18:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: jak kreslit grafy funkcí
Zdravím v tématu,
vážený kolega Rumburak napsal(a):
Ale opakuji: neznám přesné zadání úlohy a proto je možné, že se mělo řešit něco úplně jiného.
Zadání "úlohy z 1. příspěvku" je "výběr" z odkazovaného textu ↑ Alenka.Janská: - elektronická učebnice. Žluté pole na úvod 4. stránky (celkem bezdůvodně).
Výklad v učebnici se mi nezdá příliš zdařilý. Navíc se nevztahuje k problému autorky tématu.
Proto bych navrhovala v tomto tématu více nerozebírat. Můžeme se dohodnout na založení samostatného tématu. Děkuji.
Pro ↑ Alenka.Janská:
bylo by velmi vhodné, pokud bys v některém tématu uspořádala okruhy, které potřebuješ probrat k reparátu. Pokud máš pouze své poznámky (zřejmě ze sešitu z cvičení), není to přehledné, co do názvu okruhů. Alespoň takový dojem jsem nabyla po přečtení témat, co jsi založila. Je to na přeskáčku a k žádnému výsledku nepovede.
Obvykle se před reparátem dává přehled ke zkoušce a doporučená cvičení. Pokud jsi takový přehled nedostala, bylo by vhodné se zastavit za některou spolužačkou/spolužákem a poprosit o pořádné zápisky.
Podobného doporučení se Tobě již dostalo i od dalších kolegů. Jelikož působení v takových tématech by byla ztrátou času, navrhuji, abys prošla témata, co jsi založila a přidala příspěvek, zda je téma vyřešené a všemu rozumíš, nebo zda se k tématu máš v plánu vracet a proto zatím neoznačuješ za vyřešené.
Můj postup bude takový - pokud neuvidím žádnou Tvou reakci v rozpracovaných tématech, potom zamknu každé další téma, které založíš, dokud nedořešíš již rozpracovaná témata.
Děkuji za pochopení.
Jelena.
Offline