Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 07. 2011 08:19 — Editoval simonaj1 (22. 07. 2011 08:19)
faktoriál
Ahoj, potřebovala bych poradit, jestli jsem postupovala dobře nebo je nějaký lepší způsob: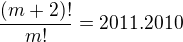
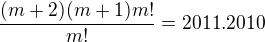 zkrátila jsem m!
zkrátila jsem m!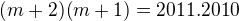
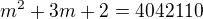
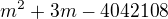 nyní jsem řešila jako kvadratickou rovnici D mi vyšel 16 168 449, po odmocnění 4021,001 zaokrouhlila jsem na 4021
nyní jsem řešila jako kvadratickou rovnici D mi vyšel 16 168 449, po odmocnění 4021,001 zaokrouhlila jsem na 4021
1. x= -2021, 2. x= 2009
ve výsledcích je 2009 takže počítám, že to mám snad dobře
potřebovala bych jen vědět, jestli se k tomu nedá dostat nějak líp
Offline
#2 22. 07. 2011 08:30
Re: faktoriál
↑ simonaj1:
Nemusíš to počítat jako kv. rci, když si uvědomíš, že zápis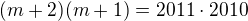
říká, že nalevo máš součin dvou po sobě jdoucích čísel a napravo také, takže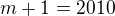 a
a 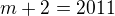
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 22. 07. 2011 08:39 — Editoval Cheop (22. 07. 2011 08:41)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: faktoriál
↑ simonaj1:
Pro podmínku 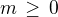
By se dala závěrečná rovnice napsat: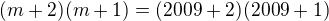 a z toho
a z toho 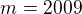
PS: Druhý kořen je -2012
Nikdo není dokonalý
Offline
#4 22. 07. 2011 17:21
Re: faktoriál
Kolegové už postup řekli, já bych jen doplnil, že je vidět, jak krásně a jednodušše lze dojít k výsledku a neudělat chybu.
Řešení kvadratickou rovnicí je tuze pěkné, avšak... dá se tam udělat chyba, kterou jsi ty udělala. Diskriminant vyjde 16 168 441 a odmocnina z něj vyjde přesně 4 021, nic se tedy zaokrouhlovat nemusí.
Tohle je tedy krásný příklad toho, že jednodušší je lepší. :-)
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
