Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 11. 06. 2008 09:42 — Editoval jelena (11. 06. 2008 14:25)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovní úlohy o pohybu
↑↑ ttopi:
Zdravim :-) zbezne jsem to prosla a tipuji to na nejaky preklep v zadani.
Pokud mas cas, tak zkus si pohrat :-) - dejme tomu, ze 14100 je dobre. 14100 se da rozlozit na 47 * 3 * 100 . 100 se pokrati s 100 v cenach listku, ted musime poskladat nasobky 10 a 9 a 8 do 141 - coz se zadanim nesedi. To je tak spis pro tebe, az pujdes na praxi do skoly :-)
↑↑ ondrax:
zkus, prosim, jeste zkontrolovat zadani. Dekuji
Offline
#34 11. 06. 2008 10:23
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovní úlohy o pohybu
↑ jelena:
To by bylo v pořádku, ale poměr je jiný než je v zadání
Mě vychází toto:
Když zachovám poměr 2:3:4
pak počet jednotlivých lístků je 12:18:24 = 54 žáci, ale celková cena lístků je pokud jsem dobře počítal 16200 Kč
Takže dle mého názoru je buď špatně poměr jednotlivých lístků nebo celková cena lístků .
Že by do 9 třídy chodil nějaký mladší žák a byl počítán jen jako 1/3 žáka?
Nikdo není dokonalý
Offline
#35 16. 06. 2008 16:23
Re: slovní úlohy o pohybu
Prosím o pomoc při vypočítání tohoto příkladu, opět se jedná záludný příklad. Závěrem roku se vždycky objeví náročné příklady, které jsou pro mě těžko řešitelné.
Můstek přes říčku je podepřen kůly.Každý kůl je zasazen 80 cm v zemi. Ve vodě je 35% jeho délky a nad vodou dvě pětiny jeho délky. Vypočítej délku kůlu. Kolik je nad vodou?
Já jsem si napsal rovnici , ale nevyšel mi výsledek
80+0,35x+2/5 x = x nevím jestli je vůbec zadání správné
Offline
#36 16. 06. 2008 16:55 — Editoval Chrpa (16. 06. 2008 16:59)
Re: slovní úlohy o pohybu
Označím x - délka celého kůlu
Pak musí platit: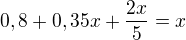 vynásobím 5 a zbavím se zlomku
vynásobím 5 a zbavím se zlomku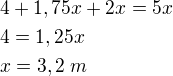
Celá délka kůlu je 3,2 metrů
Nad vodou jsou  celé délky kůlu tj
celé délky kůlu tj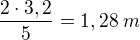
Celý kůl má délku 320 cm a nad vodou je 128 cm kůlu.
Koukám, že rovnici máš stejnou jako já.
Je můj výsledek správně nebo ne?
Offline
#39 15. 09. 2008 21:21
Re: slovní úlohy o pohybu
Zdravím všechny matematiky!
Mám tady příklad se kterým si vůbec nevím rady...a proto prosím o pomoc.
Ze dvou přístavů na řece vzdálených 24 km vypluly ve stejnou dobu proti sobě dva výletní parníky.Parník,který plul proti proudu,měl rychlost 33 km/h.
Jakou rychlostí plul po proudu druhý parník,jestliže se parníky minuly po 20 minutách plavby?
Správný výsledek je 39km/h
Prvně jsem chtěla počítat jako většinu úkolů o pohobu,na které jsem zvyklá,ale vůbec na to nemúžu přijít...chtěla jsem to počítat v1*t=v2*t
jenže mi to prostě přijde jako nesmysl,sedím nad tím už hodinu a pořád jsem na nic nepřišla...
Offline
#40 15. 09. 2008 21:42
Re: slovní úlohy o pohybu
↑ Terinka.J:
rovnice : 33*1/3 +v*1/3 = 24 ... po úpravách vyjde v = 39 ( 1/3 = 20 min)
Ok :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#41 15. 09. 2008 21:53 — Editoval Chrpa (15. 09. 2008 22:57)
Re: slovní úlohy o pohybu
Označme: v - rychlost parníku
x - rychlost proudu řeky
v+x -rychlost parníku po proudu řeky (vč. rychlosti proudu)
Ze zadání víme, že v - x = 33 km/h z toho plyne x = v - 33
Dále víme, že parníky jely protti sobě a za 20 minut tj. 1/3 hodiny urazily vzdálenost 24 km.
Z toho lze sestavit rovnici: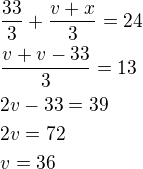
Rychlost parníku po proudu je 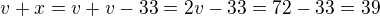 km/h
km/h
PS
Ještě mě napadlo toto: Zajímavé by bylo kdyby otázka zněla: " Vypočtěte rychlost proudu řeky".
Z mého výpočtu je to zřejmé, jinak řešení Ivany je kratší a rychlejší.
Já to počítal příliš "vědecky" a zbytečně složitě.
Offline
#43 15. 09. 2008 22:13 — Editoval Chrpa (15. 09. 2008 22:44)
Re: slovní úlohy o pohybu
↑ Ivana:
Tvá rovnice je správná, ale ty jsi spočítala celkovou rychlost parníku vč. rychlosti proudu. (takové je konečně i zadání) Moje řešení je příliš složité.
Já jsem nejdříve špatně počítal (početní chyba) a pak jsem si to špatně přečetl tedy zadání
Už je to opraveno. Já myslel, že se ptají na rychlost parníku na klidné vodě.
Offline
#44 16. 09. 2008 12:33 — Editoval Cheop (17. 09. 2008 07:55)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovní úlohy o pohybu
↑ Ivana:
Ten příklad by se dal počítat i takto (je to malá modifikace příspěvku 41)
Označme: v - rychlost parníku
x - rychlost proudu řeky
v+x -rychlost parníku po proudu řeky (vč. rychlosti proudu) - tuto rychlost máme určit.
v - x - rychlost parníku proti proudu řeky (33 km/h dle zadání)
Pak musí platit: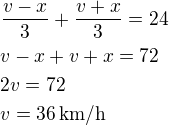
Rychlost parníku bez síly proudu (na klidné vodě je tedy 36 km/h)
Ze zadání víme, že 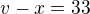 - rychlost parníku proti proudu řeky a tedy:
- rychlost parníku proti proudu řeky a tedy: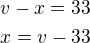 my máme určit neznámou
my máme určit neznámou 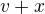 potom:
potom: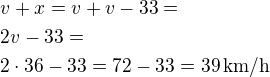
Nikdo není dokonalý
Offline
#45 16. 09. 2008 13:06
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovní úlohy o pohybu
↑ Ivana:
Na počítání pro Tebe(ale i ostatní) tady mám příklad.
Zadání:
Rybář
Rybář si vyjel na ryby proti proudu řeky motorovým člunem. Když urazil 1 km spadl mu do řeky klobouk.
Rybář pokračoval dál v cestě, ale po 5 minutách si vzpomněl, že v klobouku měl rybářský lístek. Otočil člun
a vrátil se zpátky pro ztracený klobouk. Dostihl ho přesně v místě odkud na ryby vyrazil.
Otázka: Jak rychle teče řeka? (čas potřebný k otočení člunu zanedbejte).
Nikdo není dokonalý
Offline
#46 16. 09. 2008 14:55 — Editoval ttopi (16. 09. 2008 15:10)
Re: slovní úlohy o pohybu
První tip je takový, že za dobu, co rybář jel 5 minut dál a pak cestu, kterou razil za těch 5 minut + ten celý kilometr na začátek, tak klobouk urazil 1km.
EDIT: Dobrá, pojďme na to jinak.
Od doby, kdy mu klobouk upadl, mají rybář i klobouk stejně času na to, dostat se tam, odkud rybář vyjel (to odpovídá tomu, že tam svůj klobouk dostihl).
Čas klobouku je jednoduchý, je to 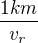 kde
kde 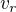 je rychlost řeky.
je rychlost řeky.
Rybář za stejný čas musí urazit 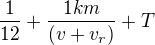 , kde je 1/12 je oněch 5 minut které jel dál, dále je to onen km zpět od místa, kde klobouk upadl, což je po proudu řeky, takže rychlost rybáře a řeky se sčítá. No ale pak je tam to T, což vyjadřuje čas, který se vracel k místu, kde mu klobouk upadl. To bohužel neumím nějak vyjádřit. Proti proudu to trvalo 5 minut, což je
, kde je 1/12 je oněch 5 minut které jel dál, dále je to onen km zpět od místa, kde klobouk upadl, což je po proudu řeky, takže rychlost rybáře a řeky se sčítá. No ale pak je tam to T, což vyjadřuje čas, který se vracel k místu, kde mu klobouk upadl. To bohužel neumím nějak vyjádřit. Proti proudu to trvalo 5 minut, což je 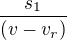 a po proudu to bude
a po proudu to bude 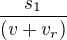 .
.
Problém je, že neznám rychlost rybáře, ani kus, který za těch 5 minut ujel, takže tady jsem v koncích. Pokusím se ještě popřemýšlet, ale tuším, že řešení bude jednodušší, než se zdá :-)
oo^0 = 1
Offline
#47 16. 09. 2008 15:08 — Editoval Cheop (16. 09. 2008 15:11)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovní úlohy o pohybu
↑ ttopi:
Když klobouk urazil vzdálenost 1 km tak člun za stejnou dobu urazil:
Vzdálenost, kterou ujel za 5 minut proti proudu + vzdálenost, kterou ujel za 5 minut po proudu + 1 km po proudu.
Nikdo není dokonalý
Offline

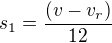 , pak ten samý úsek zpět trval
, pak ten samý úsek zpět trval 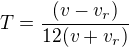 .
.