Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 06. 2008 09:15 — Editoval Cheop (05. 06. 2008 09:18)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: gon.posloupnost
Abychom mohli vypočítat člen a11 pořebujeme zjistit kvocient q
Pro n-tý člen posloupnosti an platí vztah:
an = a1*q^(n-1)
Slovně: n-tý člen je první člen krát kvocient na (n-1)
Známe čllen a4 a člen a1
a4 = a1*q^3
16 = 2*q^3
q^3 = 8
q = 2
Teď už můžeme vypočítat a11
a11 = a1*q^10
a11 = 2*2^10
a11 = 2^11
a11 = 2048
Předpokládám, že se jedná o geometrickou posloupnost a ne o goniometrickou (takovou neznám)
Nikdo není dokonalý
Offline
#5 17. 06. 2008 07:21 — Editoval Cheop (17. 06. 2008 11:07)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: gon.posloupnost
V zadání musí být zda se jedná o aritmetickou posloupnost nebo o geometrickou posloupnost.
Kdybychom vzali: jako aritmetickou posloupnost pak by platilo:
jako aritmetickou posloupnost pak by platilo:
Obecně:
V aritmetické posloupnosti jednotlivé členy této posloupnosti rostou o určitou diferenci d.
Každý následující člen aritmetické posloupnosti je o diferenci d větší nebo menší než člen předcházející (podle toho zda diference d>0 nebo d<0) V našem příkladu:

Protože diference d není celé číslo, pak bych tipoval, že bychom to měli počítat jako geometrickou posloupnost.
U geometrické posloupnosti je každý následující člen násobkem předcházejícího o tzv. kvocient q
přičemž když je q>0 pak řada roste (náš případ) pokud je q<0 pak u řada klesá nebose střídají u členů řady znaménka
Pro geometrickou posloupnost platí:

![kopírovat do textarea $40=5\cdot q^{3}\nlq^{3}=8\nlq=\sqrt[3]8\nlq=2$](/mathtex/f8/f8dea092aff364861cb1e06fd90f03bc.gif)

U druhého příkladu se bude jednat o geometrickou posloupnost s kvocientem 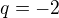


Nikdo není dokonalý
Offline
#6 17. 06. 2008 09:03
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: gon.posloupnost
Ještě ke kvocientu q geometrické řady:
Pokud je kvocient v intervalu  pak řada klesá
pak řada klesá
Pokud je kvocient v intervalu  pak řada roste
pak řada roste
Pokud je kvocient v intervalu  pak se u řady střídají znaménka
pak se u řady střídají znaménka 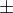
Nikdo není dokonalý
Offline
#8 17. 06. 2008 12:50
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: gon.posloupnost
↑ dedina:
Takový malý příklad na geometrickou posloupnost:
Zadání
Přičteme-li k číslům 2, 7 a 17 totéž číslo dostaneme první tři členy geometrické posloupnosti.
Určete toto číslo a geometrickou posloupnost vyjádřete vzorcem pro n-tý člen.
Nikdo není dokonalý
Offline
#12 17. 06. 2008 13:58 — Editoval Cheop (17. 06. 2008 14:25)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: gon.posloupnost
↑ dedina:
Opravdu myslíš, že 10/5 =3 nebo 20/10 = 3 ? (Možná je to u tebe jen překlep)
q = 2 a pak 
Mimochodem neodpověděl jsi na otázku, které číslo je potřeba k číslům 2,7,17 přičíst , protože to je právě číslo 3 (což ale není q)
To q určíš ze vztahu:

Nikdo není dokonalý
Offline