Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integral (s úpravou goniometrických vzorců) (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 08. 2011 10:14
integral (s úpravou goniometrických vzorců)
Hoj zdravim vas... pocitam tedka doma priklady a zrovna u tohodle prikladu jsem se nejak zasekl.. je to integral kdy nevim jak substituovat a nebo jestli mam zkouset per partes... fakt nevim jak se pohnout z mista tak prosim jen o radu cim zacit?
Zápis pro počítač: (cos((2*x))/(cos(x)^2))
Offline
- (téma jako vyřešené označil(a) zwok_toon)
#3 16. 08. 2011 10:53 Příspěvek uživatele zdenek1 byl skryt uživatelem zdenek1. Důvod: pozdě
#4 16. 08. 2011 18:38
Re: integral (s úpravou goniometrických vzorců)
tak (cos x)^2=1 - (sin x)^2
ale cos 2x = 1 - sin 2x
no ale porad nevim co bych asi dal do substituce 1/1-(sinx)^2 - sin2x/1-(sinx)^2 ==> ln|1-(sinx)^2| - **Integral** sin2x/1-(sinx)^2 a tedka per partes?
Offline
#5 16. 08. 2011 19:34
Re: integral (s úpravou goniometrických vzorců)
Radim, tedy jsem.
Dobrá rada je drahá, ta moje je zdarma.
Offline
#8 17. 08. 2011 12:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integral (s úpravou goniometrických vzorců)
↑ zwok_toon:
Zdravím,
pravděpodobně "menší dotaz" nesouvisí s úvodním dotazem. Možností je více - například  , potom lze použit podobnou úpravu, jak už zde byla diskutována nebo rozšíření čitatele a jmenovatele výrazem
, potom lze použit podobnou úpravu, jak už zde byla diskutována nebo rozšíření čitatele a jmenovatele výrazem 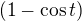
V úvodním tématu sekce VŠ jsou odkazy na užitečné online nástroje, doporučuji MAW.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integral (s úpravou goniometrických vzorců) (TOTO TÉMA JE VYŘEŠENÉ)

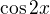 ? A jak se jinak dá zapsat
? A jak se jinak dá zapsat  ?
?