Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 08. 2011 16:52
Diferenciální rovnice, integrální počet
Dobrý den všem, mám semestrální práci, která je pro mě trochu španělská vesnice. Potřeboval bych poradit co s tím a jak postupovat. nejsem totiž nějak extra nadaný matematik. Posílám zadání i s návodem, který mi není moc jasný. Děkuji za každou pomoc
Nejprve bych se zaměřil na část jedna to oscilující řešení, může mi někdo poradit jak mám postupovat? 

Offline
#4 22. 08. 2011 10:02
Re: Diferenciální rovnice, integrální počet
Po dosazení do  by snad měly jít (nezkoušel jsem, ale návod tak radí) dopočíst ty konstanty porovnáním koeficientů u členů
by snad měly jít (nezkoušel jsem, ale návod tak radí) dopočíst ty konstanty porovnáním koeficientů u členů 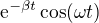 ,
,  a dalších.
a dalších.
Offline

