Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 08. 2011 13:06
Konvergence Taylorova polynomu
Dobré poledne.
Mám malou prosbu. Potřeboval bych ověřit jedno tvrzení. Bohužel při pokusu pomoci si internetem jsem narazil pouze na populární výklady a mám trochu problém najít zdroj, který by se problematikou zabýval trochu podrobněji. Můj problém je přesně tento
1) Mám dvě spojité funkce g(x) a f(x) jedné proměnné na celém R a obě mají všude všechny derivace všech řádů.
2) Existuje bod a, kde g(a) = f(a)
3) g(x) se nerovná f(x) pro všechna x > a
4) nechť b < a
A nyní moje tvrzení, které bych rád vyvrátil je následující:
Za předpokladů 1-4 platí, že existují f,g takové, že f(x) = g(x) na intervalu (b,a)
Teď naznačím, jak jsem zatím přemýšlel.
Pro spor předpokládejme, že takové funkce f,g které jsou stejné na intervalu (b,a) existují. Z uvedených předp. musí platit, že v bodě 'a' mají všechny derivace všech řádů stejné, tedy mají shodné T polynomy.a mě teda zajímá, jaké jsou podmínky, pro konvergenci T polynomu ke své funkci na intervalu, nikoliv lokálně - pro bodovou konv. je toho internet plný. Funkce se stejným T polynomem by pak byli stejné i na intervalu (a,...), pokud by měly k němu konvergovat, což je spor s bodem 3. Tou konvergencí T polynomu (že konverguje k funkci všude za přítomnosti všech derivací) si však nejsem jistý a dokonce mám pocit, že existovala nějaká podivná exponenciála, která byla protipříkladem. Mohli byste mi někdo poradit jaká je tedy přesně podmínka pro konvergenci T polynomu k funkci na nějakém intervalu?
Díky moc za každou užitečnou radu.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#2 19. 08. 2011 13:18 — Editoval halogan (19. 08. 2011 13:24)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Konvergence Taylorova polynomu
Čtu to již asi popáté, protože se mi nedaří najít ten problém. Měl bych tedy dva dotazy:
1) Nevadí trochu to rekurzivní zadání? V první bodu máte dvě funkce a pak v tvrzení máte, že za předpokladu že existují, tyto funkce existují :-) Proto mi není jasné, zda má rovnost vyplývat z předpokladů, nebo zda hledáme takové funkce, které by tu rovnost splňovaly (čtu to takto, proto návrh řešení v bodu 2).
2) V čem nevyhovují funkce, které jsou na (-oo, 0> nulové a pak x^2, resp. -x^2? a = 0, b libovolné záporné. Stále mi to vrtá hlavou.
Pokud jsem něco šeredně nepochopil, tak se omlouvám za vlézání do tématu. Je pátek, tak mi to snad prominete :-)
Edit: oprava funkce, nebyla nulová derivace u exponenciely v nule.
Offline
#3 19. 08. 2011 13:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence Taylorova polynomu
↑ rughar:
Např. funkce 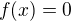 a
a  pro kladné x, jinak
pro kladné x, jinak 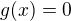 .
.
Offline
#4 19. 08. 2011 13:52 — Editoval Pavel Brožek (19. 08. 2011 14:05)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence Taylorova polynomu
↑ halogan:
2) Taková funkce nemá druhou derivaci v nule, odporuje to tedy předpokladu 1).
Edit: Myslím, že zadání bylo myšleno takto:
1) Funkce f a g jsou funkcemi jedné reálné proměnné, jsou definovány na celém R a mají všude všechny derivace všech řádů.
2) Existuje bod a, kde g(a) = f(a)
3) g(x) se nerovná f(x) pro všechna x > a
4) b < a
5) f(x) = g(x) na intervalu (b,a)
Tvrzení: Existují funkce f a g, pro které jsou splněny body 1-5.
Edit2:
↑ rughar:
Např. zde jsem našel větu
Nechť f je funkce taková, že má derivac všech řádů na nějakém okolí U bodu a. Nechť T je její Taylororova řada v a.
Jestliže existuje konstanta M taková, žepro všechna přirozená čísla N a všecha t z U, pak T konverguje (stejnoměrně) k f na U.
Pochopil jsem správně, že takovéhle věty hledáš?
Offline
#5 19. 08. 2011 16:41
Re: Konvergence Taylorova polynomu
Díky všem.
Tak zdá se, že přítomnost všech derivací implikuje stejnoměrnou konvergenci T polynomu. Tím je tvrzení, které jsem chtěl vyvrátit, vyvráceno a vše je v pořádku. Děkuji.
Co jsem zjistil, že není v pořádku, je že to opět neřeší můj konkrétní problém v diplomce, protože moje funkce jsou typu té samé (jako naschvál), jak uvedl Pavel B. v první reakci. Ta totiž v nule má pouze hodnotu, nikoliv derivace. Takže mám za sebou další (asi už tisícátý) pokus, který jednu hypotézu nenevyvrací, ale ani ji nedokazuje a můžu hledat vesele dál :-). Mám pocit, že se vesmír prostě spiknul.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#6 19. 08. 2011 18:02
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence Taylorova polynomu
↑ rughar:
Tvému příspěvku příliš nerozumím.
Přítomnost všech derivací implikuje stejnoměrnou konvergenci T polynomu.
To podle mě neplyne z ničeho, co tu padlo, a nemyslím si, že je to pravda.
Ta totiž v nule má pouze hodnotu, nikoliv derivace.
Funkce, kterou jsem uvedl, má podle mě v nule všechny derivace. A všechny jsou nulové.
Offline
#7 19. 08. 2011 18:30
Re: Konvergence Taylorova polynomu
↑ Pavel Brožek:
Nikoliv. První derivace v nule opravdu neexistuje.
, což je první derivace té funkce, v ule neexistuje. Pozor. Eistence Taylora vyžaduje jen aby tam měla derivace limitu. Podle tvojí věty už musí ty derivace existovat. To je podle mě to, co ta věta co jsi psal zcela přímo říká. Ta exponenciála atm má derivace pouze v limitě - proto existuje T polynom. Ale už nekonverguje - nemá totiž v nule derivaci zkrátka.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#8 19. 08. 2011 19:19 — Editoval Pavel Brožek (19. 08. 2011 19:32)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence Taylorova polynomu
↑ rughar:
Jak jsem psal výše, funkce g v nule nabývá hodnoty 0 (tou exponencielou je definována až pro kladná x). Derivaci je potřeba spočítat z definice.

Obě jednostranné limity se rovnají, existuje tedy limita .
.
Taylorova řada funkce g je  . Řada stejnoměrně konverguje na celém R k nulové funkci.
. Řada stejnoměrně konverguje na celém R k nulové funkci.
Offline
#9 22. 08. 2011 16:22 — Editoval rughar (22. 08. 2011 16:23)
Re: Konvergence Taylorova polynomu
↑ Pavel Brožek:
To je vlastne pravda. Zajimave je ale toto. Podle vety
Nechť f je funkce taková, že má derivac všech řádů na nějakém okolí U bodu a. Nechť T je její Taylororova řada v a.
Jestliže existuje konstanta M taková, žepro všechna přirozená čísla N a všecha t z U, pak T konverguje (stejnoměrně) k f na U.
U nasi podivne exponencialy mohu derivace v pohode omezit jednickou a presto T polynom k funkci evidentne stejnomerne nekonverguje. Neco bude podivne na te vete, ne?
1 + 1 = 1 + 1
... a nebo taky ne
Offline