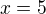Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 08. 2011 20:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: iracionální rovnice
Zdravím,
je to v pořádku.
OT: Ty si z náš tropíš žerty nebo procházíme předzářijovým přezkoušením? Děkuji.
Offline
#3 22. 08. 2011 21:01
Re: iracionální rovnice
↑ simonaj1:
Mas to dobre, ale tento priklad je peknou ukazkou, ze ked sa na zaciatku lepsie pozrieme na zadanie, tak si usetrime dost prace :)
Pod odmocninou mame x-3, cize to musi byt samozrejme nezaporne cislo, takze urcite musi platit 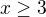 .
.
Cela lava strana bude urcite nezaporna (odmocnina zaporna nie je nikdy), takze aby platila rovnost, tak aj prava strana musi byt nezaporna, z coho zase mame 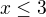 .
.
No a z tychto dvoch nerovnosti hned vidime, ze jedine cislo, ktore moze byt korenom je 3 (po dosadeni zistime, ze naozaj korenom aj je).
Offline
#6 23. 08. 2011 22:01
Re: iracionální rovnice
↑ BakyX:
Substitucia je velmi dobry napad Baky :) Dovolim si ale opravit jednu chybu z nepozornosti: v prvom riadku na pravej strane ma byt -a namiesto a.
Offline

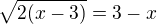 umocním obě strany rovnice
umocním obě strany rovnice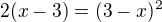
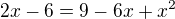
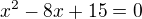

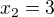


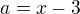 situácie veľmi sprehľadní. Stačí riešiť rovnicu:
situácie veľmi sprehľadní. Stačí riešiť rovnicu: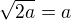
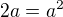
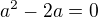
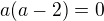
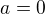 , tak
, tak 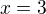
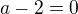 , tak
, tak