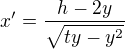Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 06. 2008 20:51
Re: Ověření maxima
No pokud se jedná o lokální maximum, tak bys mohl zkusit třeba vzít si z každé strany bodu x, jehož funkční hodnota je oním maximem, 2 velice blízké čísla y a z (nejlépe co nejbližší) a ukázat, že funkční hodnoty jsou menší než f(x). To by jí mohlo stačit :-)
oo^0 = 1
Offline
#3 18. 06. 2008 21:18
Re: Ověření maxima
Díky. Jedná se o příklad, kdy je nádoba naplněná vodou a my máme udělat otvor tak, aby voda stříkala co nejdál. Vyšlo 8,5. Toto jsem vypočítal první derivací.
Takže podle Tebe bych teď měl do funkce dosadit třeba 8,4 a 8,6 a to, že mi vyjde, že voda bude stříkat blíž, je ověření maxima? Snad jo :)
Offline
#4 18. 06. 2008 21:19
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Ověření maxima
↑ ttopi:
ve fyzice to zpravidla vyplývá z povahy věci
taky stačí ukázat že tam první derivace mění znaménko z plus na minus anebo ze tam je druhá derivace záporná
--------------------------------------
"To asi ty ses honem hlásil, co?“
„Kdepak, maminko! Já se vůbec ani nehlásil, já bysem s holkama ani nehrál, ale pan učitel řek’: Musíš!“
Offline
#5 18. 06. 2008 21:21
Re: Ověření maxima
↑ Green:
To se ověřuje podle druhé derivace funkce, pokud dosadíš to danné maximum do vzorce druhé derivace za x a dostaneš číslo, které je menší než nula, pak je ověřeno, že je to maximum = věta o postačující podmínce existence lokálního extrému(analoficky to platí i pro minimum = pokud je to číslo větší jak nula)
Offline
#6 18. 06. 2008 21:34 — Editoval ttopi (18. 06. 2008 21:40)
Re: Ověření maxima
Dobrá, podle druhé derivace to bude jistě lepší. Já jen myslel, že to chce paní profesorka jinak, než pomocí diferenciálního počtu.
Jinak ano, pokud bys dokázal, že těsně pod a těsně nad oním otvorem, kde to dostříkne do maxima, do dostříkné méně, mělo by to být hotovo.
oo^0 = 1
Offline
#11 18. 06. 2008 21:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ověření maxima
↑ Green:↑ Green:
vyznas se v tomto?
druhy radek x´´ http://forum.matweb.cz/upload/236-deriv.JPG
Offline
#12 18. 06. 2008 21:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ověření maxima
↑ VladaPi:
Zdravim :-) Mohla bych mit prosbu - zalozte si nove tema
Mate zdroj tech zadani pro kombinatoriku?
Offline
#13 18. 06. 2008 22:00
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Ověření maxima
↑ Green:
Protoze jsme ve fyzice, vzal bych to takto:
Pokud je díra moc vysoko (na úrovni hladiny) voda stéká dolů a moc daleko nedostříkne
Pokud je díra u dna, stříká sice hodně rychle, ale z nalé výšky a proto taky daleko nedostříkne
Pro tyhle krajní hodnoty je určitě délka kam to dostříkne nula.
No a optimální řešení: musí to být dostatečně vysoko, aby to dostříklo daleko, ale ne moc vysoko, protože by to zase vytíkalo pomalu. Takže z derivace určíme nulové body. Pokud by jich bylo více, musíme najít maximum, ale protože je jenom jediný kandidát, bude optimální řešení to co Vám vyšlo.
Tohle je přece fyzikální úvaha, tak to musí stačit, nebo ne?
----------------------------------------------------
„Zapla? Pán Bůh, zbylo nám tu kus kuřete a buchtičky tu jsou, trochu bílé kávy byste si měly vzít do láhve proti žízni.“
Offline
#14 18. 06. 2008 22:08
Re: Ověření maxima
Jo, přesně takhle to taky chápu- logicky. Problém je v tom, že tuto úlohu jsem dostal na matematice a proto to paní doktorka chce ověřit matematicky. Omlouvám se, pokud jsem se dříve nevyjádřil dost jasně. Už jsem tento úkol jednou odevzdal s výpočtem derivace a správným výsledkem a paní doktorka k tomu napsala "chybí ověřit, že je to maximum". Kamarád říkal, že to má být nějaká tabulka se znaménky + a -, ale víc neví... Takže asi tak.
Offline
#15 18. 06. 2008 22:12
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Ověření maxima
↑ Green:
to je to o cem pisu v prispevku cislo #4
....... taky stačí ukázat že tam první derivace mění znaménko z plus na minus .......
------------------------------------------
„Vzácná paní, Zdeňa spadla do krajáče s mlékem!“
Offline
#17 18. 06. 2008 22:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ověření maxima
↑ Green:
Tech 8,5 je odkud?
Tak, jak mas vyraz pro 1. derivaci - uprav ten vyraz tak, aby (h-2y) bylo v citateli. Nulovou hodnotu zlomku zabezpecuje citatel, z toho najdeme, ze y= h/2 je prave ta hodnota vysky, pro kterou predpokladame, ze dosah bude maximalni.
Jmenovatel bude vzdy kladny.
Do vyrazu (h-2y) dosadime za y nejakou hodnotu z intervalu (0, 1/2 h) - treba dosadime 1/3 h dostaneme vysledek kladny (znamenko 1. derivace +), pak dosadime 2/3h a dostaneme vysledek 1. derivace zaporny. Prohlasime, ze pri prechodu pres bod y=h/2 1. derivace meni znamenko z + na -, tedy tento bod je maximem.
Offline