Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 08. 2011 11:54 — Editoval Witiko (27. 08. 2011 12:11)
Generátor pseudonáhodných čísel
Dobrý den. Mějme algoritmus, který při konstantách a, b a m navrací m-dlouhou sekvenci pseudonáhodných čísel v intervalu (0; 1).
Zajímalo by mě, jak zvolit konstanty tak, abych zajistil, že při libovolném x nebude (ax + b) dělitelné m. V opačném případě by totiž algoritmus mohl navrátit 0, což není kýžené.
Offline
- (téma jako vyřešené označil(a) Witiko)
#3 28. 08. 2011 15:55 — Editoval Witiko (28. 08. 2011 15:57)
Re: Generátor pseudonáhodných čísel
Díky za odpověď. Zdá se, že tomu nejspíš tak bude, ačkoliv se mi nedaří reprodukovat myšlenkové pochody, kterými jsi k tomu došel (s hledáním využití GCD a LCM jsem měl vždy problém). Každopádně většinou jsou v generátorech pseudonáhodného šumu jako konstanty a a m volena velká prvočísla, jejichž GCD je 1. Tzn. standardem nejspíš bude, že navracená čísla jsou v intervalu <0; 1).
Offline
#4 28. 08. 2011 16:21 — Editoval FailED (28. 08. 2011 21:14)
Re: Generátor pseudonáhodných čísel
Přesně tak, jde o to, že rovnice 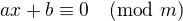 má pro a, m nesoudělná vždycky řešení.
má pro a, m nesoudělná vždycky řešení.
Kdyby existovala taková dvě  , bylo by
, bylo by 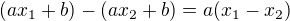 dělitelné m a tedy
dělitelné m a tedy 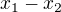 dělitelné m - tedy nutně
dělitelné m - tedy nutně  . Proto když vezmeme m po sobě jdoucích x, proběhne ax+b všechny možné zbytky po dělení m.
. Proto když vezmeme m po sobě jdoucích x, proběhne ax+b všechny možné zbytky po dělení m.
Podobně to funguje pro soudělná a, m; (ax+b) mod m potom "obskáče" všechny zbytky dělitelné GCD(a,m).
Offline
#5 29. 08. 2011 23:52 — Editoval Witiko (30. 08. 2011 00:15)
Re: Generátor pseudonáhodných čísel
↑ FailED:: Nejedná se o Tvojí chybu, ale modulární aritmetika a kongruence není součástí středoškolského učiva, což mi znemožňuje Tvé vysvětlení v celistvosti pochopit. Pokusím se do toho ale proniknout. :-)
Edit: Ok, mám základní průpravu, tzn. 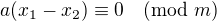 implikuje pravdivost
implikuje pravdivost 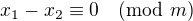 jelikož a a m jsou nesoudělné a proto musí být částí dělitelnou m
jelikož a a m jsou nesoudělné a proto musí být částí dělitelnou m  , že?
, že?
Offline
