Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 08. 2011 19:01
#3 26. 08. 2011 19:29
Re: Podivna kvadratura kruhu
↑ miso16211:
Je to len aproximácia kvadrutúry kruhu. Nemal by byť problém vypočítať chybu.
1^6 - 2^6 + 3^6 = 666
Offline
#4 26. 08. 2011 20:57
Re: Podivna kvadratura kruhu
↑ miso16211:
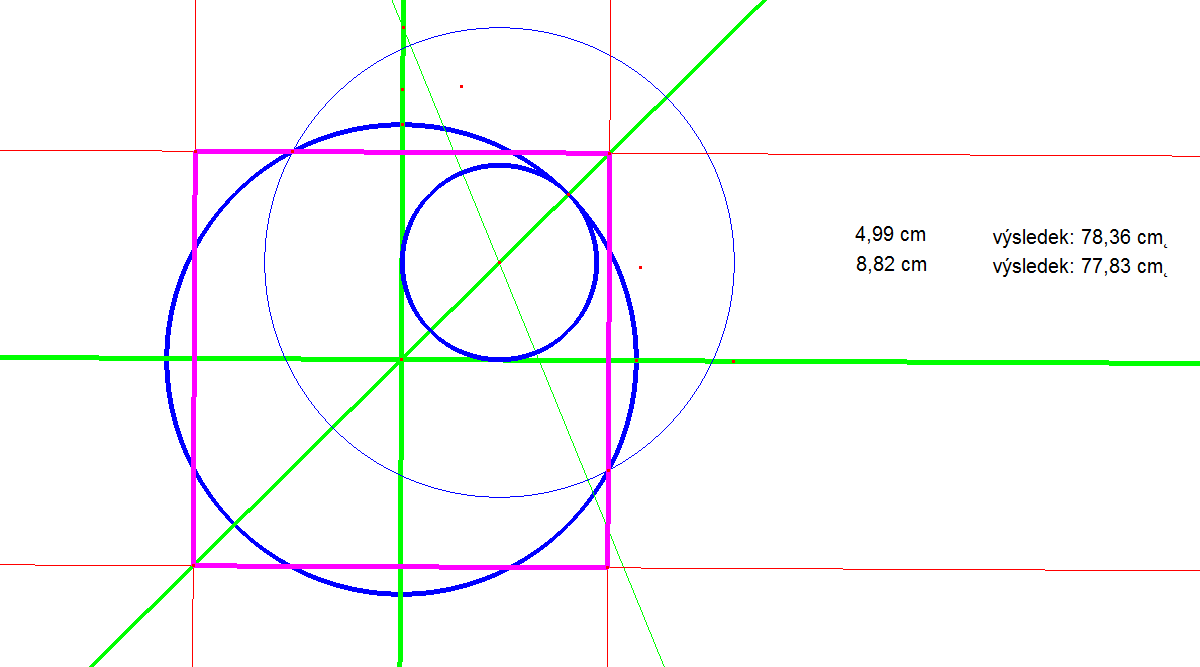
Výpočtem vychází strana čtverce přibližně 1.766407r a tedy aproximace pí na 3.12019373731, což není nic závratného.
Online
#5 31. 08. 2011 23:58 — Editoval Peppy (01. 09. 2011 00:13)
Re: Podivna kvadratura kruhu
Mal by som aj inú metódu...
Zostrojte pravouhlý trojuholník, ktorého odvesny sú 8 a 9. Od prepony odčítajte 8,9 a máte Pí na stotisíciny presne (3,14159). Zostrojením štvorca nad touto úsečkou máte Obsah štovrca . Snáď to pomôže.
Dogmatické myšlienky nikdy nezmenia svet.
Offline
#7 01. 09. 2011 01:05 — Editoval Peppy (01. 09. 2011 01:12)
Re: Podivna kvadratura kruhu
↑ Phate:
Tak to potom by sme museli mať nástroje ako dokázať rysovať iracionálne nekonečné čísla, samozrejme s podporou Pytagorovej, a Euklidových viet. Navyše keď si to zoberieme, tak to v podstate nejde fyzikálne vo vesmíre previesť, pretože neviem, ako sa dá presne narysovať nekonečné číslo. Preto v tomto ponímaní, ako hovoríš, bez aproximácie je to proste somarina. S aproximáciou sa to už dá.
// EDIT:
Euklides by mal byť šťastný, že budeme vôbec k tomu aproximovať a nevymýšľať :D. Na takú myšlienku mal prísť skôr, že sa žiadne iracionálne, tj. nekonečné číslo nedá narysovať bez aproximácie :D
Dogmatické myšlienky nikdy nezmenia svet.
Offline
#9 01. 09. 2011 01:23 — Editoval Peppy (01. 09. 2011 01:27)
Re: Podivna kvadratura kruhu
No, pí je nekonečné iracionálne číslo. Žiadne nekonečné iracionálne číslo nedokážem narysovať úsečkou AB bez aproximácie, presne o veľkosti  . Ani uhlopriečka v štvorci o strane 2 nie je na narysovanom papieri presne
. Ani uhlopriečka v štvorci o strane 2 nie je na narysovanom papieri presne  ale iba danou aproximáciou. Preto si myslím, že keby Euklides ešte trochu viacej porozmýšľal, nevytvoril by tento "konečno-nekonečný problém".
ale iba danou aproximáciou. Preto si myslím, že keby Euklides ešte trochu viacej porozmýšľal, nevytvoril by tento "konečno-nekonečný problém".
A ak neviem narysovať úsečku 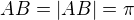 , potom neviem narysovať ani štvorec, ani kruh o strane/polomere
, potom neviem narysovať ani štvorec, ani kruh o strane/polomere 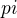 , lebo bez aproximácie to proste nejde.
, lebo bez aproximácie to proste nejde.
Dogmatické myšlienky nikdy nezmenia svet.
Offline
#11 01. 09. 2011 14:07
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Podivna kvadratura kruhu
poprve, vsetko co nakreslim na papier s ceruzkou a kruzidlom jasne ze nie je presne,
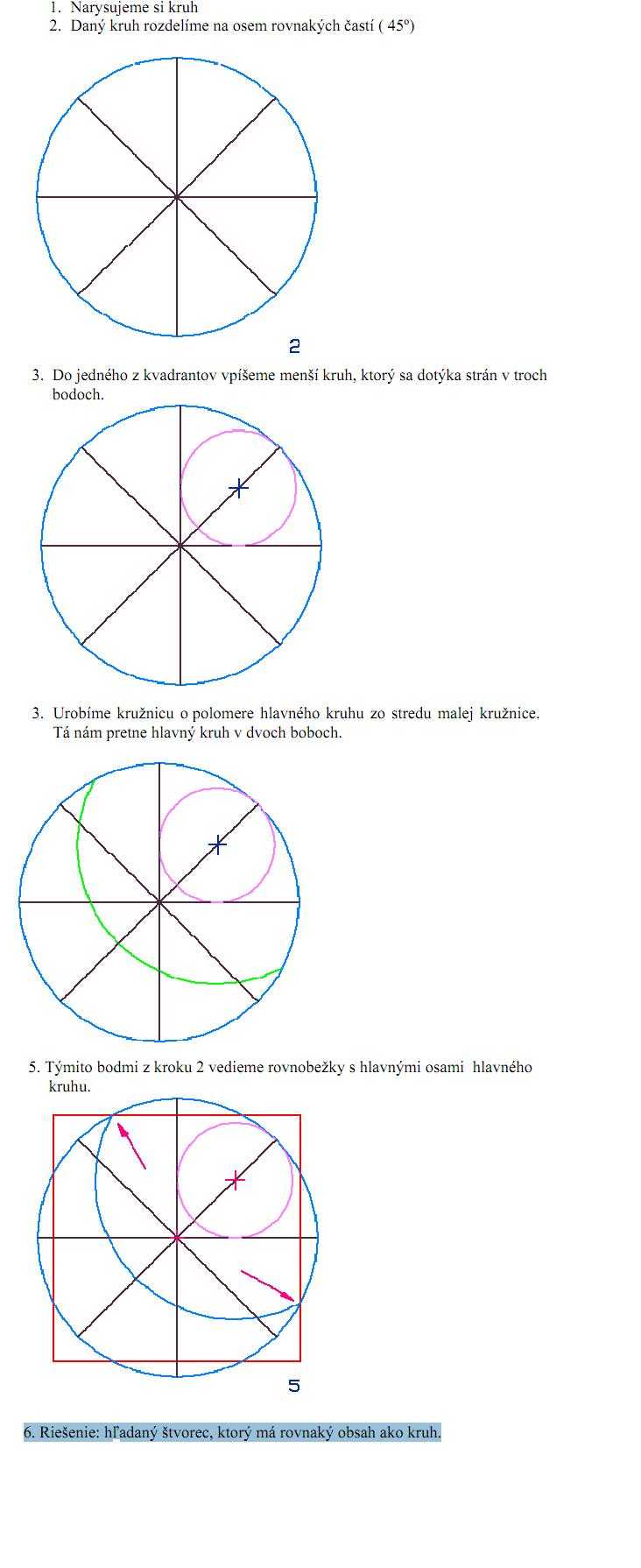
Nevieme narysovať nekonečne čislo napr. PÍ, ale vieme obsah polmesiaca preniest do stvorca - v urcitom ponimani je to nekonecné
Offline
#12 01. 09. 2011 16:44
Re: Podivna kvadratura kruhu
Teoretické konštrukcie v hlave sú síce pekné ale z toho sa architekti nenajedia :D
↑ musixx:
A potom o čo ide? Nech budem aproximovať pí nejakým zázračným spôsobom na n-miestnu presnosť, potom štvorec (o veľkosti plochy v centimetroch štvorcových), bude mať ešte väčšiu presnosť vo výpočte, geometricky sa samozrejme nič nezmení, pretože sa pohybujeme v malých jednotkách (cm), navyše pí nikdy nebude viac ako 3,2 (cm). Takže, nech je to akokoľvek - teoreticky alebo prakticky - si myslím, že Euklides zase uťal do zlého stromu.
↑ miso16211:
No, nie celkom pravda, zase ide len o aproximáciu, v podstate sa jedná o to, že nedokážeš ohraničiť nekonečné číslo hranicou (nejakou krivkou) - geometricky nenarysuješ presne žiadnu z iracionálnych hodnôt, pretože by si musel ísť do veľkosti atómov - a to teda nejde. Tu je ten rozdiel medzi geometriou a algebrou. Čím väčší štvorec by som urobil, tým viac by uhlopriečka konvergovala ku  . Teda, ak by som mal štvorec o hrane jeden kilometer, uhlopriečka bude mať
. Teda, ak by som mal štvorec o hrane jeden kilometer, uhlopriečka bude mať 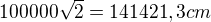 , ak by som mal štvorec hranu 1000km tak ten výsledok bude konvergovať ku
, ak by som mal štvorec hranu 1000km tak ten výsledok bude konvergovať ku 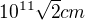 .
.
Preto fakt neviem, v čom leží ten problém. Asi ma nebudete mať radi, možno že sa na mňa Euklides hnevá. Možno zhorím v matematickom pekle, ale proste nesúhlasím s Euklidovou domienkou rysovať nekonečné čísla.
Dogmatické myšlienky nikdy nezmenia svet.
Offline
#13 01. 09. 2011 17:15
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Podivna kvadratura kruhu
Problem je ten, že ešte nikto nenarysoval rovnaky štvorec ako kruh s absolutnou presnosťou -
a nevem čo riešiš↑ Peppy:
absolutna presnosť - napr. narysujem priamku na papier, je sice rovná, ale len teoreticky, v skutočnosti je to krivka.
Offline
#17 01. 09. 2011 17:42 — Editoval jarrro (01. 09. 2011 17:50)
Re: Podivna kvadratura kruhu
↑ Peppy:myslím,že v matematike pod slovom "konštrukcia" sa rozumie to čo sa na základnej či strednej škole označuje ako "zápis konštrukcie"pozri napr. na wiki teda,že sú dva body uričtej vzdialenosti,priamka úsečka,kolmica , rovnobežka ,kružnica atď a ich prieniky.To, kde konkrétne na výkres ten bod umiestniš a s akou zastrúhanou resp. tupou ceruzkou to realizuješ je už skôr záležitosť fyziky
aj odmocnina z dvoch je iracionálna a dá sa zostrojiť napr ako uhlopriečka jednotkového štvorca to,že to nebude pri konkrétnom narysovaní presné je dané už len tým,že tie úsečky a body vidíš hoci by mali ideálne byť neviditeĺné,keďže majú nulovú šírku a pri narysovaní majú aspoň tú desatinu milimetra
MATH IS THE BEST!!!
Offline
#18 01. 09. 2011 17:54 — Editoval Peppy (01. 09. 2011 17:55)
Re: Podivna kvadratura kruhu
Peppy napsal(a):
Mal by som aj inú metódu...
Zostrojte pravouhlý trojuholník, ktorého odvesny sú 8 a 9. Od prepony odčítajte 8,9 a máte Pí na stotisíciny presne (3,14159). Zostrojením štvorca nad touto úsečkou máte Obsah štovrca . Snáď to pomôže.
Ak si dokážem predstaviť, že uhlopriečka je presne  aj na papieri, tak aj môj postup hore je presný. Proste snažím sa vám tu ukázať na realitu rozdielu medzi geometriou a algebrou.
aj na papieri, tak aj môj postup hore je presný. Proste snažím sa vám tu ukázať na realitu rozdielu medzi geometriou a algebrou.
Dogmatické myšlienky nikdy nezmenia svet.
Offline
#24 01. 09. 2011 18:16 — Editoval jarrro (01. 09. 2011 18:18)
#25 01. 09. 2011 18:24
Re: Podivna kvadratura kruhu
Peppy, problem je ze ty resis jak to narysovat s tou presnosti. Problem je spise jak tu konstrukci vubec vymyslet. Kdyz znas pythagorovu vetu, tak vis, ze pravouhly trojuhelnik o odvesnach 1 bude mit preponu odmocninu ze dvou i kdyz ji nenarysujes s tou presnosti o ktere se tu hadame. Ta uloha spociva v tom najit zpusob jak tu kvadraturu kruhu sestrojit a ne se k ni priblizit pres stroj a nejakou aproximaci.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline

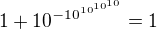 hoci tá presnosť by možno neurobila viditeľnú chybu ani pri rozmeroch vesmíru
hoci tá presnosť by možno neurobila viditeľnú chybu ani pri rozmeroch vesmíru