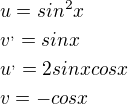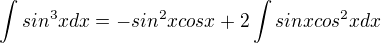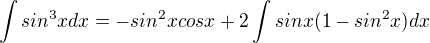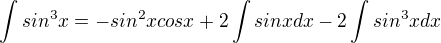Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 06. 2008 12:09
integrály
Opět potřebuji pomoc:
- (x^2 - cosx)e^2x
- (x^3 + e^x)sin2x
Obojí by mělo být pomocí per partes, začala jsem roznásobením a pak integrály z jednotlivých částí, ale vždy mi tam vyjdeintegrál z e na mocninu a s ním sinus nebo cosinus a nevím co s tím, protože integrace nebo derivace e je stále e a sinus nebo cosinus se pořád mění na cosinus nebo sinus. Tak co s tím?
Všem předem děkuji za pomoc.
Offline
#2 07. 06. 2008 12:40 — Editoval plisna (07. 06. 2008 12:49)
Re: integrály
naznacim prvni: uprav si vyraz na tvar 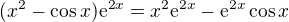 . integrovat prvni clen per partes neni problem, po dvojnasobnem pouziti polynom "zmizi" a exponenciela se jiz snadno zitregruje. druhy se udela nasledujicim zpusobem, protoze jak jsi spravne rekla, exponenciely ani sinu nebo kosinu se per partesenim nezbavis.
. integrovat prvni clen per partes neni problem, po dvojnasobnem pouziti polynom "zmizi" a exponenciela se jiz snadno zitregruje. druhy se udela nasledujicim zpusobem, protoze jak jsi spravne rekla, exponenciely ani sinu nebo kosinu se per partesenim nezbavis.
nyni si vsimni, ze se nam per partesenim znovu objevil integral 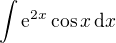 . znovu opakovat per partes by nemelo smysl - dvakrat bychom jej opakovali a opet by jsme se dostali k temuz problemu. muzeme vsak sestavit rovnici - leva strana, tj. zadani, se musi rovnat prave strane, tedy mame rovnici
. znovu opakovat per partes by nemelo smysl - dvakrat bychom jej opakovali a opet by jsme se dostali k temuz problemu. muzeme vsak sestavit rovnici - leva strana, tj. zadani, se musi rovnat prave strane, tedy mame rovnici
tedy upravami dostavame 
a konecne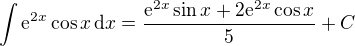
Offline
#5 21. 06. 2008 14:53
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrály
↑ Brekeke:
vsechno delas dobre. Pozor na znamenka, jinak tam zadne riziko nevidim. Napis, prosim vysledek integralu nebo si ho over tady: http://wims.unice.fr/wims/wims.cgi?sess … unction.en
Offline
#9 21. 06. 2008 18:04
Re: integrály
↑ Chrpa:
Tak to teda koukám.
Dobrá tedy. Určitě jsi si udělal vektor AB (4;1) a z vektoru na něj kolmý (-1;4) udělal obecnou rovnici výšky na stranu c=AB. Dále sis pak určitě udělal vektor AC, který je (a;b) a z vektoru na něj kolmý (-b;a) obecnou rovnici výšky na stranu AC. Máš tedy 2 rovnice a hledaný bod je vlastně průsečík těchto přímek (průsečík výšek).
Když budeš soustavu řešit, určitě ti to rozumně vyjde :-)
oo^0 = 1
Offline
#10 21. 06. 2008 18:07
Re: integrály
Když to dělám tou substitucí, tak mi to vychází 3pí (vim že je to špatně ale prosím koukněte mi na to kde dělám chybu)
3∫ (1-cos^2 x) sin x dx= 3∫ (1 - t^2) sin x ( - dt/sin x) = 3∫ - (1 - t^2) dt = 3 [ 2t ]. Pak dosadím meze a vyjde mi 3pí
cos x = t
dt = - sin x dx
dx = -dt/sin x
Offline
#12 21. 06. 2008 18:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrály
↑ Brekeke:
3∫ - (1 - t^2) dt = 3 [ 2t ] - toto neni dobre.
Ma vychazet prece -3 (t - t^3/3) pak jeste vratit substituci - misto t cos x . A az pak meze a vychazi to stejne jako kolega ↑ Chrpa: 2.
↑ Chrpa:↑ ttopi: musim trochu nastolit poradek - presunte tu debatu o vyskach tam, kde ma byt :-) Tady to zbytecne mate :-) Dekuji :-)
Offline
#13 21. 06. 2008 18:28
Re: integrály
↑ Brekeke:
Po úpravě té substituce ti vyjde inegrál: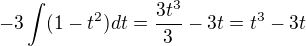
Vrátíme se k substituci  a výsledek bude:
a výsledek bude:
Pak už stačí dosadit meze a vyjde výsledek 2
Dosazením meze  vyjde 0 (cos 90 = 0)
vyjde 0 (cos 90 = 0)
Dosazením meze vyjde:
vyjde:
Offline
#14 21. 06. 2008 18:33
Re: integrály
↑ jelena:
Máš Jelenko jako vždy pravdu. Témata se nemají míchat dohromady, pak je v tom "bordel".
Substitucí je výpočet toho integrálu o hodně snažší než tou mou metodou per partes
Mimochodem kdybych pokračoval v úpravách toho mého výsledku, tak dojdu k úplně stejnému řesšení jako v případě substituce.
Na papíře už jsem to dokázal.
Offline
#15 21. 06. 2008 19:54
Re: integrály
↑ Chrpa: ↑ jelena:
Máte samozřejmě pravdu, sem to nakonci derivovala místo integrovala!
A můžete mi ještě poradit v čem pak dělám chybu, dyž mi to vychází tak jak napsal Chrpa 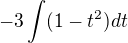 ale pak dál počítám -3 [ t - t^3/3 ] , pak -3 [cos x - cos^3 x/ 3], no a teďka dosazuju meze do tý závorky 0 - 0 - 1 - 1/3, pak násobím -3 a vychází mi 4
ale pak dál počítám -3 [ t - t^3/3 ] , pak -3 [cos x - cos^3 x/ 3], no a teďka dosazuju meze do tý závorky 0 - 0 - 1 - 1/3, pak násobím -3 a vychází mi 4
Offline
#16 21. 06. 2008 20:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrály
↑ Brekeke:
0 - 0 - 1 - 1/3 - to neni OK, bohuzel :-( chybi zavorky.
-3 [cos x - cos^3 x/ 3] = -3 [(0 - 0/3)-(1-1/3)] = -3 [0 - 2/3] = 2
OK?
Offline
#18 21. 06. 2008 20:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrály
↑ Brekeke:
Bez nas :-) ? Urcite by to mohlo byt i neco zabavnejsiho, nez matematika, ale s nami je take zabava :-)
Offline
 budeme počítat metodou per partes
budeme počítat metodou per partes