Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Báze prostoru posloupností (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 09. 2011 16:01 — Editoval OiBobik (15. 09. 2011 16:27)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Báze prostoru posloupností
Zdravím,
mám následující problém:
1) platí věta:
Důkaz kdyžtak zde:
Za povšimnutí stojí, že nikde ve formulaci (ani potom v důkazu) se nevyužívá toho, že by snad V měl být konečné dimenze. Z toho ovšem dále plyne:

Uvažme nyní vektorový prostor V všech reálných posloupností. Pak zajisté množina
 , tedy něco jako obdoba kanonické báze vektorových prostorů konečné dimenze, není bází V (podprostor jimi generovaný je množina všech reálných posloupností, které mají konečně mnoho nenulových prvků).
, tedy něco jako obdoba kanonické báze vektorových prostorů konečné dimenze, není bází V (podprostor jimi generovaný je množina všech reálných posloupností, které mají konečně mnoho nenulových prvků).No a teď můj dotaz:
1) Je to tak, nebo někde uvažuju špatně?
2) Jak tedy vypadá nějaká báze V?
3) bude taková báze vůbec spočetná?
__________________________________________________________________________
Poznámka ke značení:
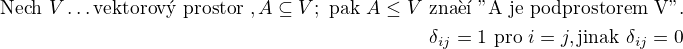
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
- (téma jako vyřešené označil(a) OiBobik)
#2 15. 09. 2011 16:07 Příspěvek uživatele Pavel Brožek byl skryt uživatelem Pavel Brožek. Důvod: Vyřešený dotaz ke značení, díky.
#3 15. 09. 2011 16:09 Příspěvek uživatele OiBobik byl skryt uživatelem OiBobik. Důvod: k dotazu ke značení
#4 15. 09. 2011 16:26
Re: Báze prostoru posloupností
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Báze prostoru posloupností (TOTO TÉMA JE VYŘEŠENÉ)
 a tedy
a tedy  . Zároveň jelikož je M průnik vektorových prostorů, tedy opět vektorový prostor, musí nutně obsahovat všechny lineární kombinace všech různých n-tic vektorů (pro lib. n) z množiny M, tedy
. Zároveň jelikož je M průnik vektorových prostorů, tedy opět vektorový prostor, musí nutně obsahovat všechny lineární kombinace všech různých n-tic vektorů (pro lib. n) z množiny M, tedy