Matematické Fórum

r2d2 · 19. 09. 2011 22:59

Ahoj, mám takový malý problém. Možná je to pokročilou hodinou(?), ale mám po úpravách tuto rovnici
$log(\frac{x+2}{4})=-log(x-1)$ a neumím se dostat k výsledku x=2 (podle wolframu). Překáží mi tam ten mínus před logaritmem. Tak jsem udělal potom toto: $log\frac{x+2}{4}=log(x-1)^\up{-1}$ , ale to wolfram říká, že výsledek je sice 2 ale i 3. Tak tedy nevím jak toto dopočítat. Snad asi jsem něco zapoměl, nevím...

Děkuji předem za radu

fojjta · 19. 09. 2011 23:13 — Editoval fojjta (19. 09. 2011 23:51)

Logaritmy při steném základu lze "krátit" (bez mínusu by to hrálo).

((:-)) · 19. 09. 2011 23:15 — Editoval ((:-)) (19. 09. 2011 23:17)

↑ r2d2:

$\log1=-\log1$

WA hovorí druhý výsledok -3, nezdá sa mi ale, že by sa dali logaritmovať záporné čísla...

r2d2 · 19. 09. 2011 23:15

↑ fojjta:promiň, ale nějak jsem nepochopil to "bez mínusu by to hrálo", myslíš jako abych dál pokračoval bez logaritmů?

r2d2 · 19. 09. 2011 23:18

↑ ((:-)):TAK TENHLE VZTAH JSEM NĚKDE CESTOU ŽIVOTEM MINUL!!! :-O DÍKY MOC, UŽ TO SEDÍ

r2d2 · 19. 09. 2011 23:21

↑ ((:-)):

P.S. - není to záporné číslo, jen převrácená hodnota ( myslím, že se tomu tak říká ) a tady je odkaz na trapný pokus jak se zbytečně zbavovat toho mínusu:-)
díky

Odkaz

((:-)) · 19. 09. 2011 23:24 — Editoval ((:-)) (19. 09. 2011 23:57)

↑ ((:-)):

Autor skryl část textu. Zobrazit/skrýt!

$\log a^{-1}=-\log a$ podľa pravidiel počítania s logaritmami, platí to pre dovolené a

r2d2 · 19. 09. 2011 23:29

↑ ((:-)):teď asi úplně nechápu kam tím míříš...

((:-)) · 19. 09. 2011 23:31 — Editoval ((:-)) (19. 09. 2011 23:33)

↑ r2d2:

neumím se dostat k výsledku x=2

ale Ty si asi mal na mysli iba tú "skúšku"...

fojjta · 19. 09. 2011 23:34 — Editoval fojjta (19. 09. 2011 23:50)

↑ r2d2:
"Krácení" jsem myslel nějak takhle:
$log(x-1)+log(x+2)=log(4) -> x^2+x-2=4$ a řešíš kvadr.rov.

edit: Děkuji za upozornění, skutečně jsem chtěl napsat "krácení".

r2d2 · 19. 09. 2011 23:35

↑ ((:-)):ano tohle pravidlo znám, ale tím že by se násobily dvě závorky by z toho vznikla zase kvadratická rovnice, a kromě toho to $log1 = -log1$ posloužilo skvěle. Divím se, že to třeba na wiki není a já to vidím a možná snad i slyším poprvé :-o

((:-)) · 19. 09. 2011 23:41 — Editoval ((:-)) (19. 09. 2011 23:44)

↑ r2d2:

Využitím vzťahu $\log a^{-1}=-\log a$ , ale v smere $-\log a=\log a^{-1}$ sa dá tá úloha vyriešiť ešte jednoduchšie...

Autor skryl část textu. Zobrazit/skrýt!

Logaritmy majú rovnaké základy a rovnajú sa, musia sa teda rovnať aj čísla, ktoré logaritmujeme...

To chcel asi povedať kolega fojjta tým "krátením"...

r2d2 · 19. 09. 2011 23:43

:-) ( veliký rozpačitý úsměv ) , vypočítaný to mám, zkoušku jsem nemyslel, jen jsem nevěděl co mám dělat s tím mínusem a co bylo zásadní neznal jsem toto $log1 = -log1$ . Jak jsem to použil příklad vyšel. Ta kvadratická rovnice by tam udělala o jeden výsledek navíc a to se mi nelíbilo.

Takže celý příklad mám:
$log(\frac{x+2}{4})=-log(x-1)$ tady je zvrat - používám $log1 = -log1$ a
$log(\frac{x+2}{4})=log(x-1)$
$\frac{x+2}{4}=x-1$
$x+2 = 4x - 4$
$-3x = -6$
$x = 2$ a vyšlo to:-)

r2d2 · 19. 09. 2011 23:45

↑ ((:-)):díky moc, ale stejně asi zůstanu u té tvojí první rady:-)

((:-)) · 19. 09. 2011 23:45 — Editoval ((:-)) (19. 09. 2011 23:52)

↑ r2d2:

Ale takto to dobre nie je, bohužiaľ...

Tá moje "rada" sa týkala v podstate "skúšky" toho WA výsledku. Tvrdenie je pravdivé, lebo 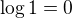$\log 1 = 0$ a aj $- \log 1 =0$ , neviem, ako si ho využil vo svojom postupe.

Vzniknutá kvadratická rovnica má dva korene, ale záporný koreň nevyhovuje, pretože záporné čísla sa nedajú logaritmovať - to je celé...

r2d2 · 19. 09. 2011 23:46 — Editoval r2d2 (19. 09. 2011 23:50)

↑ ((:-)):jakto???

takže musím použít toto $-\log a=\log a^{-1}$ a dělat to přes kvadratickou rovnici?

((:-)) · 19. 09. 2011 23:51

↑ r2d2:

Ja myslím, že v nejakej forme áno...

fojjta · 19. 09. 2011 23:56 — Editoval fojjta (20. 09. 2011 00:26)

Výraz $\log(1)=-\log(1)$ platí, ale nelze ho použít u této úlohy. Stačí se přesvědčit grafem.

edit: Opět jsem se špatně vyjádřil.

r2d2 · 19. 09. 2011 23:58 — Editoval r2d2 (20. 09. 2011 00:00)

↑ ((:-)):Tak to je škoda. Nevím tedy jak je možné že mi to vyšlo, asi nějaká náhoda.

Čili postup je mi jasný až na to, že jsem si jen neuvědomil, že -3 nemůžu použít v logaritmu.A ten log1 = -log1 jsem špatně pochopil jako tvojí radu jak to počítat a využil to jako postup, a platný vztah, který ale neplatí. On však náhodou fungoval a já to měl spočítané. i když špatným způsobem.
No to je na mě moc... uf... malé nedorozumění.

Díky ti velmi moc za pomoc

r2d2 · 19. 09. 2011 23:59

↑ fojjta:díky, už jsem to pochopil, takový malý omyl

((:-)) · 20. 09. 2011 00:02 — Editoval ((:-)) (20. 09. 2011 00:02)

↑ r2d2:

$\log1 = -\log1$

Tento vzťah platí, ale asi sa nedá využiť v tejto úlohe tak, ako si chcel...

Matematické Fórum

#1 19. 09. 2011 22:59

logaritmická rovnice

#2 19. 09. 2011 23:13 — Editoval fojjta (19. 09. 2011 23:51)

Re: logaritmická rovnice

#3 19. 09. 2011 23:15 — Editoval ((:-)) (19. 09. 2011 23:17)

Re: logaritmická rovnice

#4 19. 09. 2011 23:15

Re: logaritmická rovnice

#5 19. 09. 2011 23:18

Re: logaritmická rovnice

#6 19. 09. 2011 23:21

Re: logaritmická rovnice

#7 19. 09. 2011 23:24 — Editoval ((:-)) (19. 09. 2011 23:57)

Re: logaritmická rovnice

#8 19. 09. 2011 23:29

Re: logaritmická rovnice

#9 19. 09. 2011 23:31 — Editoval ((:-)) (19. 09. 2011 23:33)

Re: logaritmická rovnice

#10 19. 09. 2011 23:34 — Editoval fojjta (19. 09. 2011 23:50)

Re: logaritmická rovnice

#11 19. 09. 2011 23:35

Re: logaritmická rovnice

#12 19. 09. 2011 23:41 — Editoval ((:-)) (19. 09. 2011 23:44)

Re: logaritmická rovnice

#13 19. 09. 2011 23:43

Re: logaritmická rovnice

#14 19. 09. 2011 23:45

Re: logaritmická rovnice

#15 19. 09. 2011 23:45 — Editoval ((:-)) (19. 09. 2011 23:52)

Re: logaritmická rovnice

#16 19. 09. 2011 23:46 — Editoval r2d2 (19. 09. 2011 23:50)

Re: logaritmická rovnice

#17 19. 09. 2011 23:51

Re: logaritmická rovnice

#18 19. 09. 2011 23:56 — Editoval fojjta (20. 09. 2011 00:26)

Re: logaritmická rovnice

#19 19. 09. 2011 23:58 — Editoval r2d2 (20. 09. 2011 00:00)

Re: logaritmická rovnice

#20 19. 09. 2011 23:59

Re: logaritmická rovnice

#21 20. 09. 2011 00:02 — Editoval ((:-)) (20. 09. 2011 00:02)

Re: logaritmická rovnice

Zápatí