Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 25. 09. 2011 18:15

M0M0
Příspěvky: 71
Reputace:   0 
 

Zmiešaný súčin 3 vektorov

Zadanie: "Pomocou pravidiel vektorového počtu (môžete použiť aj zmiešaný súčin troch
vektorov) dokážte, že vektory v príklade č. 2 ležia v rovine. Dokážte, že vektor a x b
je kolmý na vektor c!"

Ja som sa dostal potadeto a neviem čo mi tam chýba..ale nejak mi to nepasuje..mohli by ste to plschecknuť?

http://i55.tinypic.com/280t5c2.jpg

Offline

  • (téma jako vyřešené označil(a) M0M0)

#2 25. 09. 2011 19:12

zdenek1
Administrátor
Místo: Poděbrady
Příspěvky: 12436
Reputace:   897 
Web
 

Re: Zmiešaný súčin 3 vektorov

Nechybí ti tam nic.
Smíšený součin 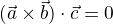$(\vec a\times\vec b)\cdot\vec c=0$, a to znamená, že vektory jsou "v jedné rovině"

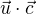spíš ti tam přebývá $\times$ ve výpočtu $\vec u\cdot\vec c$ - to je skalární součin a bývá dobrým zvykem ho označovat tečkou, nikoli křížkem

Pořádek je pro blbce, inteligent zvládá chaos!

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson