Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 27. 09. 2011 19:46
Re: Definiční obor ln(ln(arg))
↑ Jenda358:to jsem rád..uff, a ještě jedna malá otázka. Vyšlo mi, že x > -7, když bych do funkce dal -7 vypadne mi nula, je to tak?
Offline
#5 27. 09. 2011 19:57 — Editoval r2d2 (27. 09. 2011 19:57)
Re: Definiční obor ln(ln(arg))
↑ Jenda358:díky moc za výsledek/ potvrzení výpočtu, na chvilku jsem zaváhal, ale mám ten výsledek stejně a taky to chápu a to je hlavní, díky
Offline
#6 27. 09. 2011 20:00 — Editoval r2d2 (27. 09. 2011 20:07)
Re: Definiční obor ln(ln(arg))
↑ Jenda358:ještě jedna dopluňující otázka.
Teď jsem se kouknul a něco mi tam nesedí. Já mám df jako  . Myslel jsem, že -3 a 3 tam nepatří jen kvůli jmenovateli ve zlomku, ale ona ta funkce nabývá
. Myslel jsem, že -3 a 3 tam nepatří jen kvůli jmenovateli ve zlomku, ale ona ta funkce nabývá  hodnot třeba s
hodnot třeba s 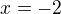 Proč?
Proč?
Offline


 je
je  a
a  není definován.
není definován. .
.