Matematické Fórum

r2d2 · 28. 09. 2011 09:46

Ahoj,
vím, že je brzo ráno a svátek, ale třeba mi někdo poradí.
Mám funkci $f(x,y) = arcsin(4x^2 +y^2)$ a potřebuju zjistit definiční obor.

Zkusil jsem si to napsat takto: (JENOM POKUS, NĚCO MI ŘÍKÁ, ŽE TO NENÍ VŮBEC SPRÁVNĚ )
$-1 \le 4x^2+y^2 \le 1$
$0 \le 4x^2+y^2 +1 \le 1$
$0 \le 4x^2+y^2 \le 0$
$0 \le 4x^2+ \le -y^2$ podmínka $y\le0$
$0 \le 2x \le y$
$0 \le x \le \frac{y}{2}$

Takže by mi z toho vycházelo, že definiční obor musí splňovat podmínky, že: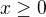
$x\ge0$ , $x \le \frac{y}{2}$ a $y \le0$

Je na tom vůbec něco správně? Anebo je to celé špatně a mám to dělat úplně jinak?
Děkuji za reakce.

Olin · 28. 09. 2011 09:59

Podmínka $-1 \le 4x^2+y^2 \le 1$ je zcela správně, její úpravy však už nikoliv. Osobně bych se raději vyvaroval úpravám "třístranné" nerovnosti, protože hned první krok, který jsi v podstatě provedl, byl, že jsi k levé a prostřední straně přičetl jedničku, ovšem pravou stranu jsi nechal tak. Spíše bych řešil zvlášť nerovnosti $-1 \le 4x^2+y^2$ a $4x^2+y^2 \le 1$ . První je triviální (stačí si uvědomit, že druhé mocniny jsou vždycky nějaké), s druhou asi moc nehneme, kromě geometrické interpretace.

r2d2 · 28. 09. 2011 10:12

↑ Olin:.. díky za odpověď. Ta první $-1 \le 4x^2+y^2$ je že x,y náleží R. Je to tak? Ale ta druhá? Vím jen, že geometricky je to elipsa, ale nějak nechápu jak s ní mám pracovat dál?

FailED · 28. 09. 2011 10:32 — Editoval FailED (28. 09. 2011 10:55)

↑ r2d2:

$f(x,y):=4x^2+y^2$ je zřejmě spojitá funkce, elipsa je uzavřená křivka, žádné jiné kořeny, než body elipsy rovnice $4x^2+y^2=0$ nemá. Uvnitř elipsy tedy může f nabývat jen kladných nebo jen záporných hodnot, vně taky - dosaď si.

Edit: ↑ Olin:
Chtěl jsem naznačit, že je potřeba uvažovat o tom, proč může být řešením vnitřek nebo venek, tady je to, pravda, snad celkem zřejmé.

Olin · 28. 09. 2011 10:39

↑ FailED:
Tak to jsem bohužel fakt nepochopil :-) Jaká rovnice má mít kořeny? Co nabývá kladných či záporných hodnot?

↑ r2d2:
Můj názor je, že se už o moc víc říct nedá. Můžeme prostě konstatovat $D(f) = \{[x, y] \in \mathbb{R}^2\colon 4x^2 + y^2 \leq 1\}$ , nebo říct, že definiční obor je elipsa (včetně vnitřku) se středem v počátku, osami rovnoběžnými se souřadnicovými a poloosami délek 1/2 a 1.

r2d2 · 28. 09. 2011 10:46

↑ Olin:Děkuji moc za výsledek. Tady se moc nechytám, jelikož kuželosečky si skoro nepamatuji. Mám mezery ze SŠ a asi je budu muset rychle doplnit. Wolfram mi ukázal graf elipsy a vnitřek je podmínka pro <=1, ale abych ten graf sestrojil, či odhadl, na to se budu muset podívat.
Díky

Matematické Fórum

#1 28. 09. 2011 09:46

Definiční obor f(x,y)=arcsin(...)

#2 28. 09. 2011 09:59

Re: Definiční obor f(x,y)=arcsin(...)

#3 28. 09. 2011 10:12

Re: Definiční obor f(x,y)=arcsin(...)

#4 28. 09. 2011 10:32 — Editoval FailED (28. 09. 2011 10:55)

Re: Definiční obor f(x,y)=arcsin(...)

#5 28. 09. 2011 10:39

Re: Definiční obor f(x,y)=arcsin(...)

#6 28. 09. 2011 10:46

Re: Definiční obor f(x,y)=arcsin(...)

Zápatí