Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kalkulacka a podiel s velkymi exponentami (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 09. 2011 16:28
Kalkulacka a podiel s velkymi exponentami
Caute
Potreboval by som pomoct ako upravit priklady ako tento, tak aby sa dali vypocitat na Casio fx-991 ES
(4,309*10^-40)*(-6,629*^-52)^6 / (9,909*10^-12)^2*(6,205*10^-16)^3
Prepacte, nebol som si isty ci by to v Tex (pri mojom skille) zobrazilo spravne, preto som to pre lepsiu priehladnost dal aspon do zatvoriek.
Vdaka za pomoc
Offline
- (téma jako vyřešené označil(a) Aikido21)
#2 30. 09. 2011 16:44
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Kalkulacka a podiel s velkymi exponentami
Buď všechno pořádně pouzávorkovat:
((4,309*10^(-40))*(-6,629*10^(-52))^6) / ((9,909*10^(-12))^2*(6,205*10^(-16))^3)
Nebo používat paměti...
Offline
#3 30. 09. 2011 16:44
Re: Kalkulacka a podiel s velkymi exponentami
↑ Aikido21:
6,629*^-52
- tady má být také *10^-52 ?
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 30. 09. 2011 16:45 — Editoval janca361 (30. 09. 2011 16:50)
- janca361

- .
- Příspěvky: 3284
Re: Kalkulacka a podiel s velkymi exponentami
↑ Aikido21:
Ahoj, v čem je problém? Zkoušela jsem to na své Casio fx-570 ES a jde to vpohodě, zadáš a výsledek.
EDIT:
Místo "/" jsem použila 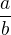 , vyhneš se tak některým závorkám.
, vyhneš se tak některým závorkám. 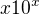 je dole uprostřed, exponent není třeba závorkovat, když je záporný. Číslo na
je dole uprostřed, exponent není třeba závorkovat, když je záporný. Číslo na  ,
, 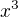 ,
,  není třeba závorkovat. Nadbytečné závorky, poku jsou obě nevadí.
není třeba závorkovat. Nadbytečné závorky, poku jsou obě nevadí.
Offline
#5 30. 09. 2011 16:49 Příspěvek uživatele janca361 byl skryt uživatelem janca361.
#6 30. 09. 2011 16:51 — Editoval found (30. 09. 2011 17:03)
Re: Kalkulacka a podiel s velkymi exponentami
(4,309*10^-40)*(-6,629*^-52)^6 / (9,909*10^-12)^2*(6,205*10^-16)^3
Je zadání myšleno takhle?
Pokud ano, pak:
Cpát do kalkulačky mocniny desítky je, dle mého, trochu padlé na hlavu. Tohle už musí být schopna spočíst jakákoliv kalkulačka (i ta, co neumí mocniny). Stačí jednoduše nacpat do kaulklačky to, co je ve zlomku, mocninu desítky už ne.
A jak udělat ty mocniny, kdyby náhodou nebylo jasno: Místo 9,909 na druhou napíši 9,909 * 9,909 a obdobně u jiných mocnin - zvládne to kalkulačky s násobením, což jsou snad všechny.
A možná tam mám nějakou numerickou chybu, občas něco přehlédnu, takže kdyby výsledek nebyl správný, tak se omlouvám, postup každopádně je lepší, než cpát původní verzi do kalkulačky.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#7 30. 09. 2011 17:25
Re: Kalkulacka a podiel s velkymi exponentami
↑ found: jj, zadanie bolo myslene presne takto. Problem bol v tom, ze mi to v tomto tvare kvoli velkosti exponentov nechcelo spocitat a ja som nevedel ako to upravit aby som to mohol dat do kalkulacky v tvare s nizsimi exponentami ale z tvojho postupu som to jasne pochopil, takze ti dakujem. :)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Kalkulacka a podiel s velkymi exponentami (TOTO TÉMA JE VYŘEŠENÉ)