Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 10. 2011 12:40
asymptoty fukce
Ahoj, nejsem schopen pohnout s tímto příkladem.
Máme určit asymptoty této funkce: 
Vyjádřil jsem si a:![kopírovat do textarea $a = \lim_{x\to\pm\infty} \left[ \frac{ x \left( \sqrt{1-\frac2x} - \sqrt{1+\frac2x} \right) }{x} \right] = \sqrt1 -\sqrt1 = 0$](/mathtex/a5/a5ee384605ddfca313ba3127241f5c49.gif)
Ale mám velký problém jak vyjádřit b:![kopírovat do textarea $b = \lim_{x\to\pm\infty} \left[ \left( \sqrt{x^2-2x} - \sqrt{x^2 + 2x} \right) - 0x \right]$](/mathtex/9f/9f86c713cf1401defb1d49b81873099b.gif) To
To  se tam myslím nedává v tomto případě, ale jistý si tím nejsem. Ale stejně nejsem schopen vypočíst limitu:
se tam myslím nedává v tomto případě, ale jistý si tím nejsem. Ale stejně nejsem schopen vypočíst limitu: ![kopírovat do textarea $\lim_{x\to\pm\infty} \left[ \sqrt{x^2-2x} - \sqrt{x^2 + 2x} \right]$](/mathtex/8d/8d195a19ec4c3649dd2ac7acb812ee33.gif) Poradí mi někdo prosím nějaký možný postup? Ve škole jsme ještě derivace nebraly. Wolfram to spočetl na 2 a -2, ale v krocích jsem viděl hodněkrát derivace a l'Hospitala. Dá se to počítat bez derivací?
Poradí mi někdo prosím nějaký možný postup? Ve škole jsme ještě derivace nebraly. Wolfram to spočetl na 2 a -2, ale v krocích jsem viděl hodněkrát derivace a l'Hospitala. Dá se to počítat bez derivací?
Offline
- (téma jako vyřešené označil(a) r2d2)
#4 01. 10. 2011 21:06 — Editoval r2d2 (01. 10. 2011 21:14)
Re: asymptoty fukce
↑ LukasM:Tak se mi to nějak povedlo, měl jsem malé zdržení, ale s počítáním nemělo nic společného. A dostal jsem se k tomuto:![kopírovat do textarea $b = -4 \lim_{x\to\pm\infty} \left[ \frac{x} {|x| \left( \sqrt{1-\frac2x} - \sqrt{1+\frac2x} \right)} \right] $](/mathtex/1b/1b6b33a9838d47fba1ff1622929f8ea7.gif) A jestli se nemílým, tak výsledná hodnota se odvíjí od znaménka x v absolutní hodnotě.
A jestli se nemílým, tak výsledná hodnota se odvíjí od znaménka x v absolutní hodnotě.
Pakliže je  tak
tak
a pakliže  tak
tak
Myslím, že to tak je.
Díky moc za radu
Offline

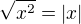 . To jsi vlastně při počítání a zapomněl, ale zachránilo tě to, že 0=-0.
. To jsi vlastně při počítání a zapomněl, ale zachránilo tě to, že 0=-0.