Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární zobrazení (projekce) (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 06. 2008 11:32
Lineární zobrazení (projekce)
Ahojda, mám příklad, se kterým si nevím vůbec rady. Byl by tu někdo, kdo by mě ho celý spočítal a vysvětlil prosím? Nebo není někde na netu nějaký program, který to vypočítá a ukáže i postup?
Př. Lineární zobrazení U V2(R) -> V2(R) je projekcí V2(R) na osu y, v lineárním zobrazení T V2(R) -> V2(R) je T(2,3) = (3,9) T(-1,2) = (-5,-1)
a) určete všechny vektory β Є V2(R), které se ve složeném zobrazení T*U zobrazí na vektor (10,20)
b) určete jádro Ker (T^-1)*U
Offline
#2 30. 06. 2008 16:15 — Editoval Marian (30. 06. 2008 16:21)
Re: Lineární zobrazení (projekce)
Projekce (tzv. komponenta) na osu y, tedy zobrazeni U, je dano takto:
U zobrazeni T je znamo, ze T(2,3)=(3,9) a T(-1,2)=(-5,-1). Zjistime jeste, kam se zobrazi bazicke vektory (0,1) a (1,0). Protoze zobrazeni T je linearni (tedy homogenni a aditivni), z faktu
(0,7)=(2,3)+2*(-1,2)
mame
Podobne z identity
(7,0)=2*(2,3)-3*(-1,2)
je
Odtud snadno
Podobne se urci i inverzni zobrazeni T^-1 k zobrzeni T. Bude
(a) Slozene zobrazeni 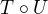 lze take zapsat jako
lze take zapsat jako 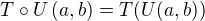 . Z vlastnosti vyse je ale
. Z vlastnosti vyse je ale
Neexistuje vsak zadne takove realne cislo b, aby platilo (-b,b)=(10,20). Tudiz neexistuje zadny vektor β Є V2(R), pro nez plati zadane podminky.
(b) Zobrazeni (T^-1*U) je toto
Proto
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární zobrazení (projekce) (TOTO TÉMA JE VYŘEŠENÉ)
